Appendix-B
Complex Algebra
The real numbers such as 5, −3, \(\frac{7}{11}\),\(\pi\), e, and so on, which may be used to measure distances in one direction or another from a fixed point.
But in reality we deal with numbers that satisfies the equations that can not be categorized as real numbers but are imaginary numbers.
Imaginary numbers add a new dimension to our number system. To deal with imaginary numbers, we introduce a new element, j, having the following property
\[j^2 = −1~~~~~~or~~~~~j=\sqrt{-1}~~~~~~(B.1)\] Thus, we have \(j^3 = −j, j^4 = 1, j^5 = j\), and so on. Using equation B.1, we can find the solutions to equation \(a^2+9=0\) are \(a = \pm j3\).
A complex number (indicated in boldface notation) can be expressed in the form
\(\textbf A = a + jb ~~~~~~ (B.2)\)
where a and b are real numbers. The complex number \(\textbf A\) has a real part a and an imaginary part b, which can be expressed as
a = Re\(\textbf A\) b = Im\(\textbf A\)
The complex number a + jb can be represented on a rectangular coordinate plane, called the complex plane, by interpreting it as a point (a, b). That is, the horizontal coordinate is a in real axis, and the vertical coordinate is b in imaginary axis, as shown in Figure B.1. The complex number \(\textbf A\) = a + jb can also be uniquely located in the complex plane by specifying the distance r along a straight line from the origin and the angle \(\theta\), which this line makes with the real axis, as shown in Figure B.1.
From the right triangle of Figure B.1, we can see that
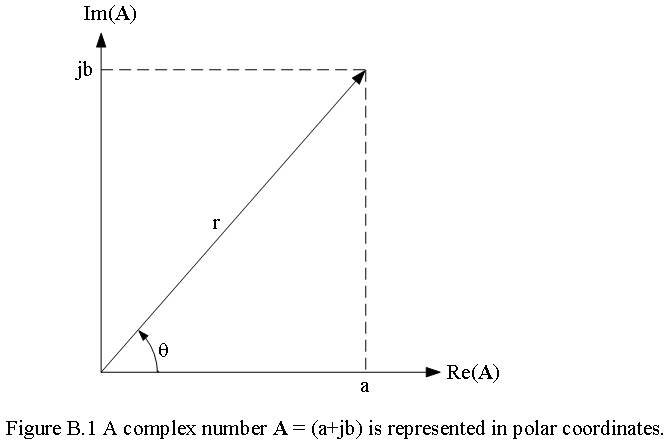
\[r = \sqrt{a^2 + b^2}\]
\[θ = tan^{-1}\frac{b}{a}\] a = r \(cos\theta\)
b = r \(sin\theta\)
Then we can represent a complex number by the expression
\(\textbf A\) = a+jb = r \(cos\theta\)+r \(sin\theta\)=\(re^{jθ} = r\angle{\theta}\)~~~~ (B.3)
which is called the polar form of the complex number. The number r is called the magnitude (or amplitude), and the number \(\theta\) is called the angle (or argument). The two numbers are usually denoted by r = |A| and \(θ = argA = \angle A\).
Given a complex number \(\textbf A\) = a + jb, the complex conjugate of A, denoted by the symbol \(\textbf A^*\), is defined by the following equalities:
ReA* = ReA ImA* = −ImA
That is, the sign of the imaginary part is reversed in the complex conjugate.
EXAMPLE B.1 Convert the complex number A = 3 - j4 to its polar form.
Solution:
\[r = \sqrt{3^2 + (-4)^2}=\sqrt{25}=5\] \[\theta = tan^{-1}\frac{-4}{3}=-53.13^o\] \[\textbf A = r\angle\theta=5\angle -53.13^o\]
Example B.2 Convert the number \(A = 4\angle(−30^o)\) to its complex form.
Solution:
\[a = rcos\theta = 4cos(-30^o)=4\sqrt{3}/2=2\sqrt{3}\]
\[b = rsin\theta = 4sin(-30^o)=-4\frac{1}{2}=-2\]
Thus, \(\textbf A = 2\sqrt{3}-2j\)
Addition and subtraction of two complex numbers:
\[(a_1 + jb_1) + (a_2 + jb_2) = (a_1 + a_2) + j(b_1 + b_2)~~~~~(B.3)\] \[(a_1 + jb_1) − (a_2 + jb_2) = (a_1 − a_2) + j(b_1 − b_2)~~~~~(B.4)\] Multiplication of complex numbers in polar form follows the law of exponents. That is, the magnitude of the product is the product of the individual magnitudes, and the angle of the product is the sum of the individual angles, as shown below.
\[(\textbf A)(\textbf B) = (Ae^{j\theta} )(Be^{j\phi}) = ABe^{j(\theta+\phi)} = AB\angle(\theta + \phi)~~~~~ (B.5)\] Division of complex numbers in polar form follows the law of exponents. That is, the magnitude of the quotient is the quotient of the magnitudes, and the angle of the quotient is the difference of the angles, as shown in equation B.6.
\[\frac{\textbf A}{\textbf B}=\frac{Ae^{j\theta}}{Be^{j\phi}}=\frac{A\angle\theta}{B\angle\phi}=\frac{A}{B}\angle(\theta-\phi)~~~~~(B.6)\] EXAMPLE B.3 Perform the following operations, given that A = 2 + j3 and B = 5 − j4.
- A+ B (b) A− B (c) 2A+ 3B
Solution:
A+ B = (2 + 5) + j[3 + (−4)] = 7 − j
A− B = (2 − 5) + j[3 − (−4)] = −3 + j7
(c), 2A = 4 + j6 and 3B = 15 − j12.
Thus, 2A+ 3B = (4 + 15) + j[6 + (−12)] = 19 − j6
EXAMPLE B.4 Perform the following operations in both rectangular and polar form, given that A = 3 + j3 and B = 1 + j\(\sqrt{3}\). (a) AB (b) A/B
Solution:
- In rectangular form: AB = (3 + j3)(1 + j\(\sqrt{3}\)) = \((3-3\sqrt{3})+j(3+3\sqrt{3})\)
To obtain the answer in polar form, we need to convert A and B to their polar forms:
\[A = 3\sqrt{2}e^{j45^o}=3\sqrt{2}\angle45^o\]
\[B = \sqrt{4}e^{j60^o}=2\angle60^o\]
Thus, \(AB = (3\sqrt{2}e^{j45^o})(\sqrt{4}e^{j60^o)}=6\sqrt{2}\angle105^o\)
- To find A/B in rectangular form, we can multiply A and B by B*.
\[\frac{A}{B}=\frac{3+j3}{1+j\sqrt{3}}\frac{1-j\sqrt{3}}{1-j\sqrt{3}}=\frac{3+3\sqrt{3}+j(3-3\sqrt{3})}{4}\] In polar form, the same operation may be performed as follows:
\[\frac{A}{B}=\frac{3\sqrt{2}\angle45^o}{2\angle60^o}=\frac{3\sqrt{2}}{2}\angle(45^o-60^o)=\frac{3\sqrt{2}}{2}\angle(-15^o)\] Euler’s Identity:
This formula extends the usual definition of the exponential function to allow for complex numbers as arguments. Euler’s identity states that
\[e^{j\theta} = cos\theta + jsin\theta ~~~~~(B.7)\]
All the standard trigonometry formulas in the complex plane are direct consequences of Euler’s identity. The two important formulas are
\[cos\theta = \frac{e^{jθ} + e^{−jθ}}{2}~~~~~(B.8)\] \[sin\theta = \frac{e^{jθ} - e^{−jθ}}{2j}~~~~~(B.9)\] EXAMPLE B.5 Using Euler’s formula, show that \(sin θ = (e^{j\theta} − e^{−j\theta})/2j.\)
Solution:
\[(e^{j\theta} − e^{−j\theta})/2j=(cos\theta+jsin\theta − cos\theta+jsin\theta)/2j=sin\theta\] EXAMPLE B.6 In a certain AC circuit, V = ZI, where \(Z = 7.75\angle90^o\) and I = \(2\angle−45^o\). Find V.
Solution:
V = ZI = \(Z = (7.75\angle90^o)(2\angle−45^o)=15.50\angle45^o\)
EXAMPLE B.7 In a certain AC circuit, V = ZI, where Z = \(5\angle82^o\) and V = \(30\angle45^o\). Find I.
Solution:
I = \(\frac{V}{Z}=\frac{30\angle45^o}{5\angle82^o}=6\angle(-37^o)\)