Chapter 8 Magnetic Fields

Learning Objectives:

In this chapter you will basically learn:

\(\bullet\) Learn how charged particle motion in electric and magnetic fields.

\(\bullet\) Learn what produces a magnetic field.

\(\bullet\) Learn how to define magnetic field, \(\vec B\).

\(\bullet\) Learn how to discovery electron, using crossed fields.

\(\bullet\) Learn the Hall effect and its application in determining the carrier types and their concentrations.

\(\bullet\) Learn how a circulating charged particle is used in Mass Spectrometer, Cyclotrons and Synchrotrons.

\(\bullet\) Learn the magnetic force on a current-carrying wire.

\(\bullet\) Learn torque on a current loop.

8.1 Charged Particle Motion in Electric and Magnetic Fields

Consider a particle of mass \(m\) and electric charge \(q\) moving in the uniform electric and magnetic fields, \({\vec E}\) and \({\vec B}\). Suppose that the fields are perpendicular to one another), so that \({\vec E}\cdot{\vec B} = 0\).

The force acting on the particle is given by the familiar Lorentz force:

\[\begin{equation} {\vec F} = q\,\left({\vec E} + {\vec v}\times{\vec B}\right), \tag{8.1} \end{equation}\]

where \({\vec v}\) is the particle’s instantaneous velocity. Hence, from Newton’s second law, the particle’s equation of motion can be written

\[\begin{equation} m\,\frac{d{\vec v}}{dt} = q\,\left({\vec E} + {\vec v}\times{\vec B}\right). \tag{8.2} \end{equation}\]

In absence of the electric field \(\vec E\) we can write the magnetic force as follows:

\[\begin{equation} {\vec F_B} = q\left({\vec v}\times{\vec B}\right). \tag{8.3} \end{equation}\]

Therefore, the magnetic force on the particle is equal to the charge q times the cross product of its velocity \(\vec v\) and the magnetic field \(\vec B\) (all measured in the same reference frame). Using the vector cross product, we can write the magnitude of as

\[\begin{equation} F_B = |q|\left(vB\sin\phi\right) \tag{8.4} \end{equation}\]

8.2 What Produces a Magnetic Field?:

In chapter-2, we learned an electric field is produced by an electric charge. Analogously, we could expect that a magnetic field must be produced by a magnetic charge. Although individual magnetic charges (called magnetic monopoles) are predicted by certain theories, but the existence of magnetic monopoles has not been confirmed. How then are magnetic fields produced?

There are two ways we can produce magnetic field. One way is to use moving electrically charged particles, such as a current in a wire, to make an electromagnet. The current produces a magnetic field that can be used, for example, to control a computer hard drive or to sort scrap metal. In Chapter 9, we will discuss the magnetic field due to a current.

The other way to produce a magnetic field is by means of elementary particles such as electrons because these particles have an intrinsic magnetic field around them. That is, the magnetic field is a basic characteristic of each particle just as mass and electric charge (or lack of charge) are basic characteristics. As we discuss in Chapter 12, the magnetic fields of the electrons in certain materials add together to give a net magnetic field around the material. Such addition is the reason why a permanent magnet, the type used to hang refrigerator notes, has a permanent magnetic field. In other materials, the magnetic fields of the electrons cancel out, giving no net magnetic field surrounding the material.

8.3 The Definition of \(\vec{B}\) , Crossed Fields:

We determined the electric field \(\vec E\) at a point by putting a test particle of charge q at rest at that point and measuring the electric force \(\vec F_B\) acting on the particle. We then defined as

\[\begin{equation} {\vec E} = \frac{\vec F_E}{q}, \tag{8.5} \end{equation}\]

A similar definition can be deduced to define magnetic field \(\vec B\)if we could find the existence of a magnetic monopole. Due to non-existence of magnetic monopole we must define \(\vec B\) in terms of the magnetic force exerted on a moving electrically charged test particle as we discussed in Eq. 8-3.

\[B=\frac{F_B}{|q|v}\] where q is the electric charge of the particle. The SI unit for that follows from Eqs. 8-3 and 8-4 is the newton per coulomb-meter per second. For convenience, this is called the tesla (T):

\[1~tesla=1~T=1\frac{N}{A.m}\] An earlier (non-SI) unit for \(\vec B\), still in common use, is the gauss (G), and 1 tesla = \(10^4\) gauss.

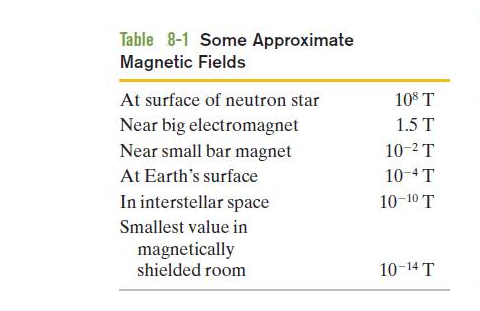
Table 8-1 lists some example magnetic fields including the Earth’s magnetic field near its surface is about \(10^{-4} T~or~100~ \mu T)\).

8.4 Discovery of the Electron, Crossed Fields:

8.5 The Hall Effect:

In a Cathode Ray Tube (CRT) or in an oscilloscope a beam of electrons in a vacuum can be deflected by a magnetic field. Similarly, it is possible to deflect the drifting conduction electrons in a copper wire or in a copper strip by applying a magnetic field. In 1879, Edwin H. Hall, then a 24-year-old graduate student at the Johns Hopkins University, showed that charge carriers can be either positively or negatively charged. He also showed how to measure the number of such carriers per unit volume of the conductor.

We investigate the Hall effect by studying the motion of the free electrons along a metallic strip of width d in a constant magnetic field (Figure 8.1).

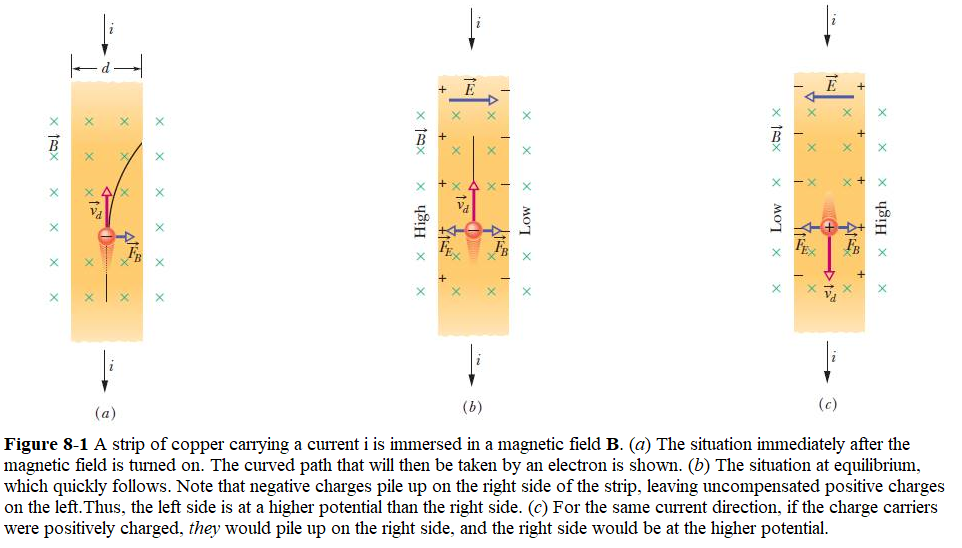
The electrons are moving from left to right, so the magnetic force they experience pushes them to the bottom edge of the strip. This leaves an excess of positive charge at the top edge of the strip, resulting in an electric field E directed from top to bottom. The charge concentration at both edges builds up until the electric force on the electrons in one direction is balanced by the magnetic force on them in the opposite direction. Equilibrium is reached when:

\[\begin{equation} eE=ev_{\mathrm{d}}B \tag{8.6} \end{equation}\]

where e is the magnitude of the electron charge, \(v_{\mathrm{d}}\) is the drift speed of the electrons, and E is the magnitude of the electric field created by the separated charge. Solving this for the drift speed results in

\[\begin{equation} v_{\mathrm{d}}=\frac{E}{B} \tag{8.7} \end{equation}\]

Going back to the Hall effect, if the current in the strip is i, then from Current and Resistance, we know that

\[\begin{equation} i=nev_{\mathrm{d}}A \tag{8.8} \end{equation}\]

where n is the number of charge carriers per volume and A is the cross-sectional area of the strip. Combining the equations for v_{} and i results in

\[\begin{equation} i=ne\left(\frac{E}{B}\right)A \tag{8.9} \end{equation}\]

The field E is related to the potential difference V between the edges of the strip by

\[\begin{equation} E=\frac{V}{d} \tag{8.10} \end{equation}\]

The quantity V is called the Hall potential and can be measured with a voltmeter. Finally, combining the equations for i and E gives us

\[\begin{equation} V=\frac{Bid}{neA}=\frac{Bid}{neld}=\frac{Bi}{nel} \tag{8.11} \end{equation}\]

where the upper edge of the strip in Figure 8.6.1 is positive with respect to the lower edge.

We can also combine 8.6.1 and 8.6.5 to get an expression for the Hall voltage in terms of the magnetic field:

\[\begin{equation} V = v_{\mathrm{d}}Bd \tag{8.12} \end{equation}\]

What if the charge carriers are positive, as in Figure 8.6.1? For the same current i, the magnitude of V is still given by 8.6.6. However, the upper edge is now negative with respect to the lower edge. Therefore, by simply measuring the sign of V, we can determine the sign of the majority charge carriers in a metal.

Hall potential measurements show that electrons are the dominant charge carriers in most metals. However, Hall potentials indicate that for a few metals, such as tungsten, beryllium, and many semiconductors, the majority of charge carriers are positive. It turns out that conduction by positive charge is caused by the migration of missing electron sites (called holes) on ions, a phenomenon studied in the field of condensed matter physics.

The Hall effect can be used to measure magnetic fields. If a material with a known density of charge carriers n is placed in a magnetic field and V is measured, then the magnetic field can be determined from 8.6.6. In research laboratories where the fields of electromagnets used for precise measurements have to be extremely steady, a “Hall probe” is commonly used as part of an electronic circuit that regulates the field.

8.6 A Circulating Charged Particle:

Figure 8-2 shows a beam of electrons is projected into a chamber by an electron gun G.The electrons enter in the plane of the page with speed v and then move in a region of uniform magnetic field \(\vec F_B=q\vec v\times\vec B\) directed out of that plane. As a result, a magnetic force continuously deflects the electrons, and because \(\vec v\) and \(\vec B\) are always perpendicular to each other, this deflection causes the electrons to follow a circular path.

Uniform circular motion is balanced with magnetic force gives us

\[\begin{equation} |q|vB = \frac{mv^2}{r} \tag{8.13} \end{equation}\]

Solving for r,we find the radius of the circular path as

\[\begin{equation} r = \frac{mv}{|q|B}~~~(radius) \tag{8.14} \end{equation}\]

The period T (the time for one full revolution) is equal to the circumference divided by the speed:

\[\begin{equation} T = \frac{2\pi r}{v}=\frac{2\pi mv}{v |q|B}=\frac{2\pi m}{|q|B}~~~(period) \tag{8.15} \end{equation}\]

The frequency f (the number of revolutions per unit time) is

\[\begin{equation} f = \frac{1}{T}=\frac{qB}{2\pi m}~~~(frequency) \tag{8.16} \end{equation}\]

The angular frequency v of the motion is then

\[\begin{equation} \omega = 2\pi f =\frac{|q|B}{m}~~~(angular~frequency) \tag{8.17} \end{equation}\]

The quantities T, f, and \(\omega\) do not depend on the speed of the particle (provided the speed is much less than the speed of light). Fast particles move in large circles and slow ones in small circles, but all particles with the same charge-to-mass ratio !q!/mtake the same time T (the period) to complete one round trip. Using Eq. 8-3, you can show that if you are looking in the direction of , the direction of rotation for a positive particle is always counterclockwise, and the direction for a negative particle is always clockwise.

8.7 Mass Spectrometer, Cyclotrons and Synchrotrons:

The mass spectrometer is a device that separates ions based on the various charge-to-mass ratios. Ions are produced at a source that are first sent through a velocity selector, where the magnetic force is equally balanced with the electric force. The initially stationary ion is accelerated by the electric field due to a potential difference V. The ion leaves S and enters a separator chamber in which a uniform magnetic field is perpendicular to the path of the ion. A wide detector lines the bottom wall of the chamber, and the causes the ion to move in a semicircle with radius r and thus strike the detector.

Sample Problem 8.1 A uniform circular motion as shown in Fig. 8-1 of a charged particle in a magnetic field of B = 80.000 mT, V = 1000.0 V, and ions of charge \(q = 1.6022 \times 10^{-19}\) C strike the detector at a point that lies at \(x = 1.6254 ~m\). What is the mass m of the individual ions, in atomic mass units (\(1 u = 1.6605 \times 10^{-27} kg)\)?

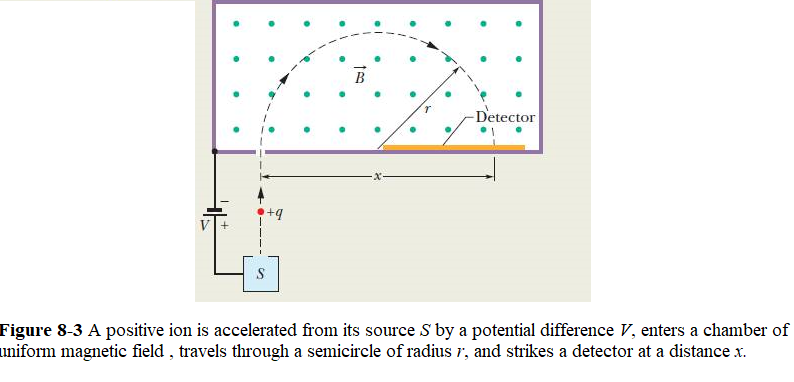
Solution If we now write the conservation of mechanical energy as \(\Delta K + \Delta U = 0\), \[\frac{1}{2}mv^2-qV= 0\] \[v=\sqrt \frac{2qV}{m}\] Substituting this value for v into Eq. 8-14 gives us

\[r=\frac {mv}{qB}=\frac{m}{qB}\sqrt\frac{2qV}{m}=\frac{1}{B}\sqrt\frac{2mV}{q}\] Thus, \[x=2r=\frac{2}{B}\sqrt\frac{2mV}{q}\] Solving this for m and substituting the given data yield

\[m=\frac{B^2qx^2}{8V}=\frac{(0.080000~T)^2(1.6022 \times 10^{-19} C)(1.6254~m)^2}{8\times 1000~V}=3.3863\times 10^{-25}~kg=203.93~u~(Answer)\] Cyclotron: Fig. 8-4 shows the Lawrence’s 60-inch cyclotron, with magnet poles 60 inches (5 feet, 1.5 meters) in diameter, at the University of California Lawrence Radiation Laboratory, Berkeley, in August, 1939, the most powerful accelerator in the world at the time.

Suppose that a proton, injected by source S at the center of the cyclotron in Fig. 8-5, initially moves toward a negatively charged dee. It will accelerate toward this dee and enter it. Once inside, it is shielded from electric fields by the copper walls of the dee; that is, the electric field does not enter the dee.The magnetic field, however, is not screened by the (nonmagnetic) copper dee, so the proton moves in a circular path whose radius, which depends on its speed, is given by Eq. 8-5 (\(r = \frac {mv}{B}\)).

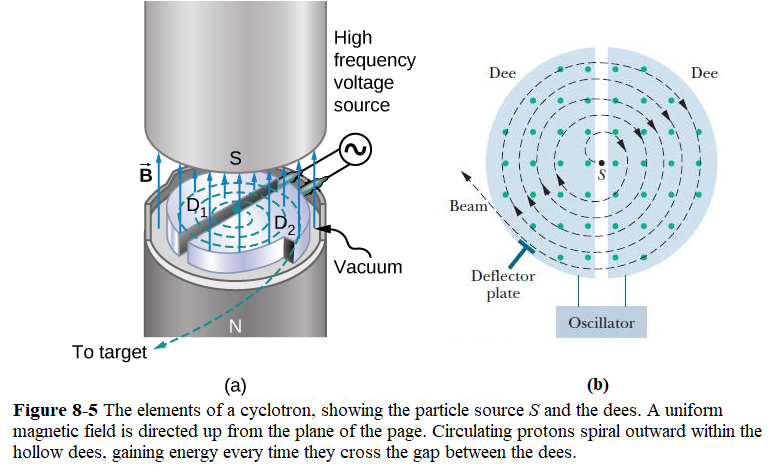
Particle energy: In a cyclotron a particle such as proton or alpha particle can be accelerated to speeds much less than the speed of light in the nonrelativistic region. For nonrelativistic particles, the particles reach their maximum energy at the periphery of the dees, where the radius of their path is \({\displaystyle r\;=\;R}\) the radius of the dees. Equating these two forces

\({\displaystyle {mv^{2} \over R}=qvB\;}\) \({\displaystyle v={qBR \over m}\,}\)

So the output energy of the particles is

\[\begin{equation} {\displaystyle E={1 \over 2}mv^{2}={\frac {q^{2}B^{2}R^{2}}{2m}}\;} \tag{8.18} \end{equation}\]

Therefore, the limit to the cyclotron’s output energy for a given type of particle is the strength of the magnetic field \({\displaystyle B}\), which is limited to about 2 T for ferromagnetic electromagnets, and the radius of the dees \({\displaystyle R}\), which is determined by the diameter of the magnet’s pole pieces. So very large magnets were constructed for cyclotrons, culminating in Lawrence’s 1946 synchrocyclotron, which had pole pieces 4.67 m (184 in) (15.3 feet) in diameter.

Synchrocyclotron: A synchrocyclotron is a cyclotron in which the frequency of the driving RF electric field is being adjusted to consider the relativistic effects as the particles velocity begins to approach the speed of light. This is in contrast to the classical cyclotron, where the frequency remains constant.

\[\begin{equation} {\displaystyle f={\frac {f_{0}}{\gamma }}={f_{0}}{\sqrt {1-\beta ^{2}}}} \tag{8.19} \end{equation}\]

where \(f_{0}\) is the classical cyclotron frequency and \(\beta ={\frac {v}{c}}\) is the relative velocity of the particle beam. The rest mass of an electron is \(511~keV/c^2\), so the frequency correction is 1% for a magnetic vacuum tube with a 5.11 kV direct current accelerating voltage. The proton mass is nearly two thousand times the electron mass, so the 1% correction energy is about 9 MeV, which is sufficient to induce nuclear reactions.

EXAMPLE 8.1 A cyclotron used to accelerate proton \(\left(m=1.67\times10^{-27}~\mathrm{kg}\right., \left.q=1.6\times10^{-19}~\mathrm{C}\right)\) has a radius of \(0.50~\mathrm{m}\) and a magnetic field of \(1.8~\mathrm{T}\). (a) What is the period of revolution of the alpha-particles? (b) What is their maximum kinetic energy?

Solution: a. By identifying the mass, charge, and magnetic field in the problem, we can calculate the period:

\[T=\frac{2\pi m}{qB}=\frac{2\pi\left(1.67\times10^{-27}~\mathrm{kg}\right)}{\left(1.6\times10^{-19}~\mathrm{C}\right)(1.8~\mathrm{T})}=3.64\times10^{-8}~\mathrm{s}.\]

2. Using Eqn.8-18, we can calculate the maximum kinetic energy:

\[\begin{eqnarray} \frac{1}{2}m{v_{\mathrm{max}}}^2&=&\frac{q^2B^2R^2}{2m}=\frac{\left(1.6\times10^{-19}~\mathrm{C}\right)^2(1.8~\mathrm{T})^2(0.50~\mathrm{m})^2}{2(1.67\times10^{-27}~\mathrm{kg})}\\&=&9.93\times10^{-12}~\mathrm{J}=62~\mathrm{MeV} \end{eqnarray}\]

8.8 Magnetic Force on a Current-Carrying Wire:

Consider a length L of the wire in Fig. 8-6. All the conduction electrons in this section of wire will drift past plane xx in Fig. 8-1 in a time \(t = \frac{L}{v_d}\).Thus, in that time a charge given by

\[q = it=\frac{iL}{v_d}\] will pass through that plane. Substituting this into Eq. 8-4 yields

\[F_B=qv_dB\sin\phi=\frac{iL}{v_d}v_dB \sin90^\circ=iLB\]

Note that this equation gives the magnetic force that acts on a length L of straight wire carrying a current i and immersed in a uniform magnetic field \(\vec B\)that is perpendicular to the wire.

If the magnetic field is not perpendicular to the wire, as in Fig. 8-6, the magnetic force is given by a generalization of the above equation \(F_B=iLB\):

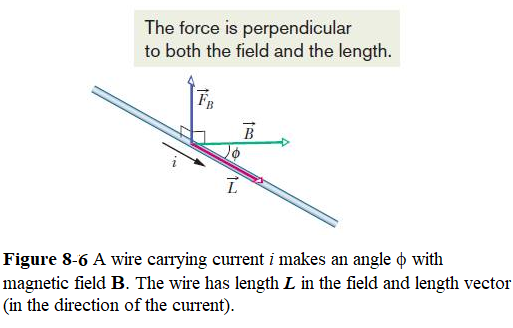
\[\begin{equation} \vec F_B = i\vec L \times \vec B \tag{8.20} \end{equation}\]

Sample Problem 8.2 A straight, horizontal length of copper wire has a current i = 28 A through it. What are the magnitude and direction of the minimum magnetic field \(\vec B\) needed to suspend the wire—that is, to balance the gravitational force on it? The linear density (mass per unit length) of the wire is 46.6 g/m.

Solution:

\[\vec F_B=\vec F_g\] \[iLB\sin\phi=mg\]

\[B_{min}=\frac{mg}{iL\sin\phi}=\frac{(m/L)g}{i\sin90^\circ}=\frac{(46.6\times10^{-3}~kg/m)(9.8~m/s^2)}{28~A}=1.6\times10^{-2}~T\]

8.9 Torque on a Current Loop:

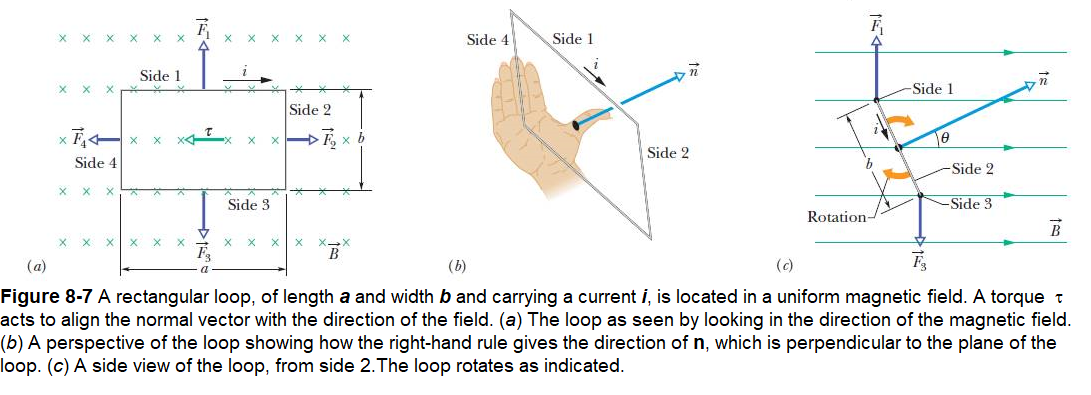
The net force on the loop is the vector sum of the forces acting on its four sides. For side 2 the vector in Eq. 8-20 points in the direction of the current and has magnitude b.The angle between \(\vec L\)and \(\vec B\) for side 2 (see Fig.8-7c) is \((90^0-\theta)\).Thus, the magnitude of the force acting on side 2 is:

\[\begin{equation} F_2=ibB\sin(90^{\circ}-\theta)=ibB\cos\theta\ \tag{8.21} \end{equation}\]

You can show that the force \(\vec F_4\) acting on side 4 has the same magnitude as \(\vec F_2\) but the opposite direction. Thus, \(\vec F_2\) and \(\vec F_4\) cancel out exactly. Their net force is zero and, because their common line of action is through the center of the loop, their net torque is also zero.

\[\begin{equation} F_4=-ibB\sin(90^{\circ}+\theta)=-ibB\cos\theta \tag{8.22} \end{equation}\]

The situation is different for sides 1 and 3. For them,\(\vec L\) is perpendicular to \(\vec B\), so the forces \(\vec F_1\)and \(\vec F_3\) have the common magnitude iaB. Because these two forces have opposite directions, they do not tend to move the loop up or down. However, as Fig. 8-7c shows, these two forces do not share the same line of action; so they do produce a net torque. The torque tends to rotate the loop so as to align its normal vector \(\vec n\) with the direction of the magnetic field \(\vec B\). That torque has moment arm \((b/2)sin\theta\) about the central axis of the loop.The magnitude \(\tau'\)( of the torque due to forces \(\vec F_1\)and \(\vec F_3\) is then (see Fig. 8-7c)

\[\begin{equation} \tau'=(iaB)\frac{b}{2}sin\theta+(iaB)\frac{b}{2}sin\theta=(iabB)~sin\theta \tag{8.23} \end{equation}\]

Suppose we replace the single loop of current with a coil of N loops, or turns then the torque become \(\tau = N\tau'=NiabB~sin\theta=(NiA)~Bsin\theta\), in which A(= ab) is the area enclosed by the coil. The quantity \(NiA\) is called the magnetic dipole moment.

The magnetic dipole moment is a vector quantity and is defined as:

\[\begin{equation} \vec \mu =NiA\vec n \tag{8.24} \end{equation}\]

where \(\vec n\) is a unit vector directed perpendicular to the plane of the loop (see Figure 8.7).

EXAMPLE 8.2 A circular current loop of radius \(2.0~\mathrm{cm}\) carries a current of \(2.0~\mathrm{mA}\). (a) What is the magnitude of its magnetic dipole moment? (b) If the dipole is oriented at 30 degrees to a uniform magnetic field of magnitude \(0.50~\mathrm{T}\), what is the magnitude of the torque it experiences and what is its potential energy?

Solution: a. The magnetic moment \(\mu\) is calculated by the current times the area of the loop or \(\pi r^2\).

\[\mu=iA=(2.0\times10^{-3}~\mathrm{A})(\pi(0.02~\mathrm{m})^2)=2.5\times10^{-6}~\mathrm{A}\cdot\mathrm{m}^2\]

2. The torque and potential energy are calculated by identifying the magnetic moment, magnetic field, and the angle between these two vectors. The calculations of these quantities are:

\[\begin{eqnarray} \tau=\left|\vec \mu\times \vec B\right|=\mu B~sin\theta=\left(2.5\times10^{-6}~A-m^2\right)(0.50~T)\sin(30^{\circ})=6.3\times10^{-7}~N\cdot m \end{eqnarray}\]

\[\begin{eqnarray} U=-\vec \mu \cdot \vec B=-\mu B \cos\theta =-\left(2.5\times10^{-6}~A\cdot m^2\right)(0.50~T)\cos(30^{\circ})= -1.1\times10^{-6}~J \end{eqnarray}\]

Solved Problems Magnetic Fields

1. [3] An electron that has an instantaneous velocity of \[\vec v = (2.0\times 10^6~m/s)\hat i+ (3.0\times 10^6~m/s)\hat j\] is moving through the uniform magnetic field \(\vec B = (0.030~T)\hat i-(0.15~T)\hat j\)(a) Find the force on the electron due to the magnetic field. (b) Repeat your calculation for a proton having the same velocity.

2. [5] An electron moves through a uniform magnetic field given by \(\vec B = B_x\hat i+(3B_x)\hat j\). At a particular instant, the electron has velocity \(\vec v = (2.0\hat i + 4.0\hat j)~m/s\) and the magnetic force acting on it is \((6.4\times 10^{-19}~N)\hat k\). Find \(B_x\).

3. [7] An electron has an initial velocity of \(12.0\hat j+ 15.0\hat k)~km/s\) and a constant acceleration of \((2.0\times 10^{12}~m/s^2)\hat i\) in a region in which uniform electric and magnetic fields are present. If \(\vec B = (400~\mu T)\hat i\), find the electric field \(\vec E\).

4. [11] An ion source is producing \(^6Li\) ions, which have charge +e and mass \(9.99 \times 10^{-27}\) kg. The ions are accelerated by a potential difference of 10 kV and pass horizontally into a region in which there is a uniform vertical magnetic field of magnitude B = 1.2 T. Calculate the strength of the smallest electric field, to be set up over the same region, that will allow the \(^6Li\) ions to pass through undeflected.

5. [15] A conducting rectangular solid of dimensions \(d_x\) = 5.00 m, \(d_y\) = 3.00 m, and \(d_z\) = 2.00 m moves with a constant velocity \(\vec v =(20.0 m/s)\hat i\) through a uniform magnetic field \(30~mT\hat j\) (Fig. 28-35). What are the resulting (a) electric field within the solid, in unit-vector notation, and (b) potential difference across the solid?

6. [27] A mass spectrometer (Fig. 28-12) is used to separate uranium ions of mass \(3.92 \times 10^{-25}\) kg and charge \(3.20 \times 10^{-19}\) C from related species. The ions are accelerated through a potential difference of 100 kV and then pass into a uniform magnetic field, where they are bent in a path of radius 1.00 m. After traveling through \(180^\circ\) and passing through a slit of width 1.00 mm and height 1.00 cm, they are collected in a cup. (a) What is the magnitude of the (perpendicular) magnetic field in the separator? If the machine is used to separate out 100 mg of material per hour, calculate (b) the current of the desired ions in the machine and (c) the thermal energy produced in the cup in 1.00 h.

7. [37] Estimate the total path length traveled by a deuteron in a cyclotron of radius 53 cm and operating frequency 12 MHz during the (entire) acceleration process. Assume that the accelerating potential between the dees is 80 kV.

8. [46] In Fig. 28-44, a metal wire of mass m 24.1 mg can slide with negligible friction on two horizontal parallel rails separated by distance d = 2.56 cm. The track lies in a vertical uniform magnetic field of magnitude 56.3 mT. At time t = 0, device G is connected to the rails, producing a constant current i = 9.13 mA in the wire and rails (even as the wire moves). At t = 61.1 ms, what are the wire’s (a) speed and (b) direction of motion (left or right)?

9. [51] Figure 28-46 shows a wood cylinder of mass m = 0.250 kg and length L = 0.100 m, with N = 10.0 turns of wire wrapped around it longitudinally, so that the plane of the wire coil contains the long central axis of the cylinder. The cylinder is released on a plane inclined at an angle \(\theta\) to the horizontal, with the plane of the coil parallel to the incline plane. If there is a vertical uniform magnetic field of magnitude 0.500 T, what is the least current i through the coil that keeps the cylinder from rolling down the plane?

10. [62] In Fig. 28-51a, two concentric coils, lying in the same plane, carry currents in opposite directions. The current in the larger coil 1 is fixed. Current \(i_2\) in coil 2 can be varied. Figure 28-51b gives the net magnetic moment of the two-coil system as a function of \(i_2\). The vertical axis scale is set by \(\mu_{net,s} =2.0\times 10^{-5}~A.m^2\) and the horizontal axis scale is set by \(i_{2s}\)= 10.0 mA. If the current in coil 2 is then reversed, what is the magnitude of the net magnetic moment of the two-coil system when \(i_2\) = 7.0 mA?

Problems Magnetic Fields

Section 8-1 Magnetic Fields and the Definition of \(\vec B\)

1. [1] A proton traveling at \(23.0^\circ\) with respect to the direction of a magnetic field of strength 2.60 mT experiences a magnetic force of \(6.50 \times 10^{-17}\) N. Calculate (a) the proton’s speed and (b) its kinetic energy in electron-volts.

2. [2] A particle of mass 10 g and charge 80 \(\mu C\) moves through a uniform magnetic field, in a region where the free-fall acceleration is \(-9.8\hat j~m/s^2\). The velocity of the particle is a constant \(20\hat i~km/s\), which is perpendicular to the magnetic field. What, then, is the magnetic field?

3. [4] An alpha particle travels at a velocity of magnitude 550 m/s through a uniform magnetic field of magnitude 0.045 T. (An alpha particle has a charge of \(+3.2 \times 10^{-19}\) C and a mass of \(6.6 \times 10^{-27}\) kg. The angle between and is \(52^\circ\). What is the magnitude of (a) the force acting on the particle due to the field and

2. the acceleration of the particle due to \(\vec F_B\)? (c) Does the speed of the particle increase, decrease, or remain the same?

Section 8-2 Crossed Fields: Discovery of the Electron

4. [9] In Fig. 28-32, an electron accelerated from rest through potential difference \(V_1 = 1.00\) kV enters the gap between two parallel plates having separation d = 20.0 mm and potential difference \(V_2\) = 100 V.The lower plate is at the lower potential. Neglect fringing and assume that the electron’s velocity vector is perpendicular to the electric field vector between the plates. In unit-vector notation, what uniform magnetic field allows the electron to travel in a straight line in the gap?

Section 8-3 Crossed Fields: The Hall Effect

5. [14] A metal strip 6.50 cm long, 0.850 cm wide, and 0.760 mm thick moves with constant velocity through a uniform magnetic field B = 1.20 \(\mu T\) directed perpendicular to the strip, as shown in Fig. 28-34. A potential difference of 3.90 mV is measured between points x and y across the strip. Calculate the speed v.

Section 8-4 A Circulating Charged Particle

6. [22] In a nuclear experiment a proton with kinetic energy 1.0 MeV moves in a circular path in a uniform magnetic field. What energy must (a) an alpha particle (q = +2e, m = 4.0 u) and (b) a deuteron (q = +e, m = 2.0 u) have if they are to circulate in the same circular path?

7. [24] An electron is accelerated from rest by a potential difference of 350 V. It then enters a uniform magnetic field of magnitude 200 mT with its velocity perpendicular to the field. Calculate

1. the speed of the electron and (b) the radius of its path in the magnetic field.

8. [34] An electron follows a helical path in a uniform magnetic field given by \(\vec B = (20\hat i-50\hat j-30 \hat k)mT\). At time t = 0, the electron’s velocity is given by \(\vec v = (20\hat i-30\hat j+ 50\hat k)~m/s\). (a) What is the angle \(\phi\) between \(\vec v\) and \(\vec B\)? The electron’s velocity changes with time. Do (b) its speed and (c) the angle \(\phi\) change with time? (d) What is the radius of the helical path?

Section 8-5 Cyclotrons and Synchrotrons

9. [38] In a certain cyclotron a proton moves in a circle of radius 0.500 m. The magnitude of the magnetic field is 1.20 T. (a) What is the oscillator frequency? (b) What is the kinetic energy of the proton, in electron-volts?

8-6 Magnetic Force on a Current-Carrying Wire

10. [41] A 13.0 g wire of length L = 62.0 cm is suspended by a pair of flexible leads in a uniform magnetic field of magnitude 0.440 T (Fig. 28-41).What are the (a) magnitude and (b) direction (left or right) of the current required to remove the tension in the supporting leads?

11. [44] Figure 28-43 shows a wire ring of radius a = 1.8 cm that is perpendicular to the general direction of a radially symmetric, diverging magnetic field.The magnetic field at the ring is everywhere of the same magnitude B = 3.4 mT, and its direction at the ring everywhere makes an angle \(\theta = 20^\circ\) with a normal to the plane of the ring. The twisted lead wires have no effect on the problem. Find the magnitude of the force the field exerts on the ring if the ring carries a current i = 4.6 mA.

Section 8-7 Torque on a Current Loop

12. [49] Figure 28-45 shows a rectangular 20-turn coil of wire, of dimensions 10 cm by 5.0 cm. It carries a current of 0.10 A and is hinged along one long side. It is mounted in the xy plane, at angle \(\theta\) = \(30^\circ\) to the direction of a uniform magnetic field of magnitude 0.50 T. In unit-vector notation, what is the torque acting on the coil about the hinge line?

Section 8-8 The Magnetic Dipole Moment

13. [54] A magnetic dipole with a dipole moment of magnitude 0.020 J/T is released from rest in a uniform magnetic field of magnitude 52 mT. The rotation of the dipole due to the magnetic force on it is unimpeded. When the dipole rotates through the orientation where its dipole moment is aligned with the magnetic field, its kinetic energy is 0.80 mJ. (a) What is the initial angle between the dipole moment and the magnetic field? (b) What is the angle when the dipole is next (momentarily) at rest?

14. [61] The coil in Fig. 28-50 carries current i = 2.00 A in the direction indicated, is parallel to an xz plane, has 3.00 turns and an area of \(4.00 \times 10^{-3}~ m^2\), and lies in a uniform magnetic field \(\vec B = (2.00\hat i-3.00\hat j-4.00\hat k)\)mT. What are (a) the orientation energy of the coil in the magnetic field and (b) the torque (in unit-vector notation) on the coil due to the magnetic field?