Chapter 3 Gauss’ Law

Learning Objectives: In this chapter you will basically learn:

\(\bullet\) Learn how Gauss’ law relates the electric field at points on a closed surface to the net charge enclosed by that surface.

\(\bullet\) Learn how to calculate the net flux \(\Phi\) through a closed surface, by integrating the dot product of the electric field vector \(\vec E\) and the area vector \(d\vec A\)over the full surface.

\(\bullet\) Apply Gauss’ law to relate the net flux & through a closed surface to the net enclosed charge qenc.

\(\bullet\) Learn how Gauss’ law is used to find the electric field magnitude E near an isolated conducting surface with a uniform surface charge density \(\sigma\).

\(\bullet\) Learn how Gauss’ law is used to derive the electric field magnitude outside a line of charge or a cylindrical surface (such as a plastic rod) with a uniform linear charge density \(\lambda\).

\(\bullet\) Learn how Gauss’ law can be used to find the electric field magnitude inside a cylindrical nonconducting surface (such as a plastic rod) with a uniform volume charge density \(\rho\).

\(\bullet\) Apply Gauss’ law to derive the electric field magnitude E near a large, flat, nonconducting surface with a uniform surface charge density \(\sigma\).

\(\bullet\) Learn that a shell of uniform charge attracts or repels a charged particle that is outside the shell as if all the shell’s charge is concentrated at the center of the shell.

3.1 Electric Flux:

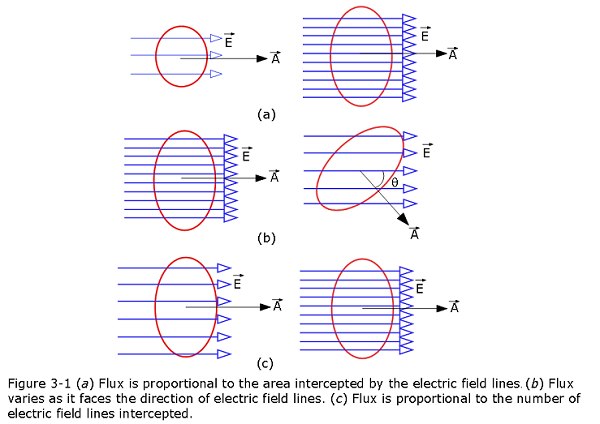
Flux means flow, in this case the flow of electric field. Electric flux, originates from an electric charge, that may be thought of as the number of electric lines of force (or electric field lines) that intersect a given area. Electric field lines are considered to originate on positive electric charges and to terminate on negative charges. Without any net charge within a closed surface, every field line directed into the surface continues through the interior and is directed outward elsewhere on the surface result in zero net or total electric flux. If a net charge is contained inside a closed surface, the total flux through the surface is proportional to the enclosed charge, positive if it is positive, negative if it is negative.

An inward piercing field is negative flux. An outward piercing field is positive flux. A skimming field is zero flux as can be seen in Fig.3-1.

Mathematically, flux can be expressed as

\[\begin{equation} \Phi = \oint {\vec E.d\vec A} \space\space (net~flux) \tag{3.1} \end{equation}\]

Example Problem 3-1:

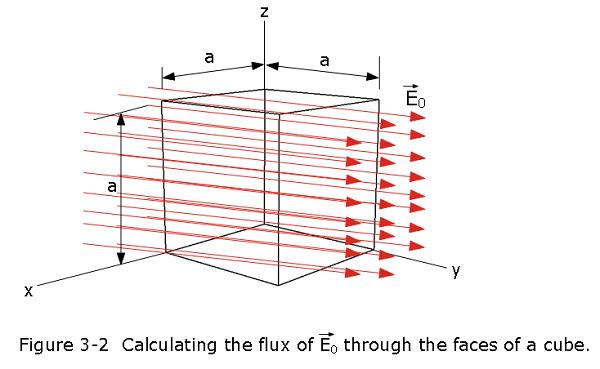
A constant electric field of magnitude \(E_0\) points in the direction of the positive y-axis (Figure 3-2). What is the electric flux through a cube with sides a in the (a) xz-plane and in the (b) yz-plane?

Solution:

1. Using Eq. 3-1, we can split the integral into six separate open integrals one for each face of the cube. For xz-plane or left plane we can write

\[\Phi_{left} = \int {\vec E.d\vec A}=\int {\hat j E_0.(-\hat jd\vec A)}= -E_0\int dA= -E_0a^2\] \[\Phi_{right} = \int {\vec E.d\vec A}=\int {\hat j E_0.(\hat jd\vec A)}= E_0\int dA= E_0a^2\] Therefore, the net flux through the left and right planes in the xz-plane will cancel each other and the net flux becomes zero through xz-plane.

\[\Phi_{xz} = \Phi_{left}+\Phi_{right} = -E_0a^2+E_0a^2=0\space (Answer)\]

2. For the yz-plane we have front and back planes that contributes to 0 because electric field and area vectors are perpendicular to each other. Thus,

\[\Phi_{back} = \int {\vec E.d\vec A}=\int {\hat j E_0.(\hat id\vec A)}= 0\]

\[\Phi_{back} = \int {\vec E.d\vec A}=\int {\hat j E_0.(-\hat id\vec A)}= 0\] \[\Phi_{yz} = \Phi_{front}+\Phi_{back} = 0+0=0\space (Answer)\] Example Problem 3-2:

Figure 3-3 shows a Gaussian surface in the form of a closed cylinder (a Gaussian cylinder or G-cylinder) of radius R and length L. It lies in an electric field that radially outward as given by \(\vec E(\vec r) = E_0\frac{r^2}{r_0^2}\hat r\). What is the net flux \(\Phi\) of the electric field through the cylinder?

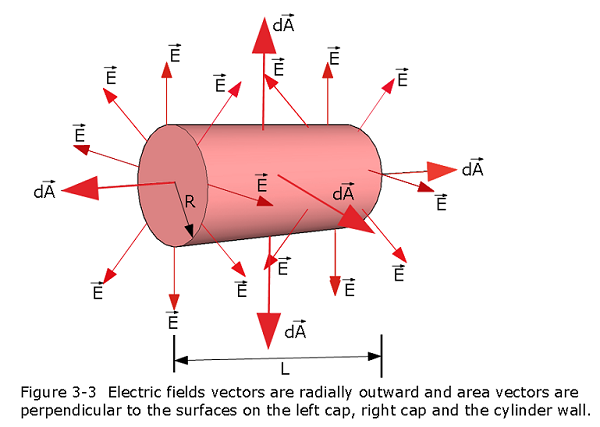
Solution:

\[\Phi_{net}=\Phi_{left}+\Phi_{right}+\Phi_{wall}\] \[\Phi_{net}=\int EdAcos90^\circ+\int EdAcos90^\circ+\int_0^L E_0\frac{R^2}{r_0^2}\hat r.\hat r2\pi Rdx\] \[\Phi_{net}=\frac{2\pi E_0R^3L}{r_0^2}\space (Answer)\]

3.2 Gauss’ Law:

Gauss’ law relates the net flux \(\Phi\) of an electric field through a closed surface (a Gaussian surface) to the net charge \(q_{net}\) that is enclosed by that surface. It tells us that

\[\begin{equation} \varepsilon_0\Phi = q_{enc} \space\space (Gauss'~Law) \tag{3.2} \end{equation}\]

\[\begin{equation} \varepsilon_0\oint {\vec E.d\vec A} = q_{enc} \space\space (Gauss'~Law) \tag{3.3} \end{equation}\]

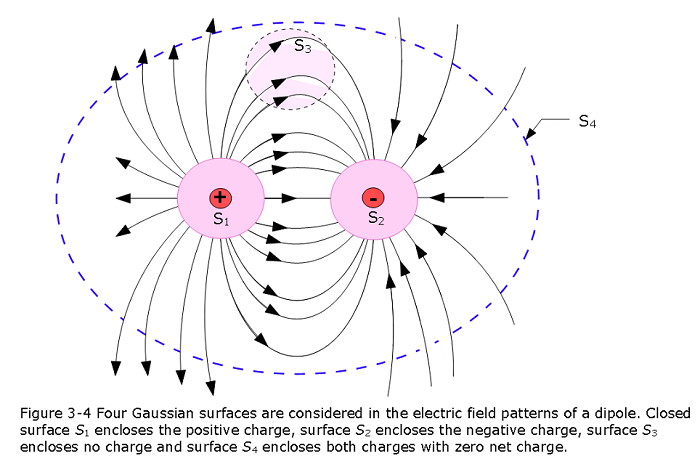
In Figure 3-4 a dipole is considered with two charges that are equal in magnitude but opposite in sign, and the field lines describing the electric fields the particles set up in the surrounding space. Four closed Gaussian surfaces are considered. Closed surface \(S_1\) encloses the positive charge, surface \(S_2\) encloses the negative charge, surface \(S_3\) encloses no charge and surface \(S_4\) encloses both charges with zero net charge.

3.3 Gauss’ Law and Coulomb’s Law:

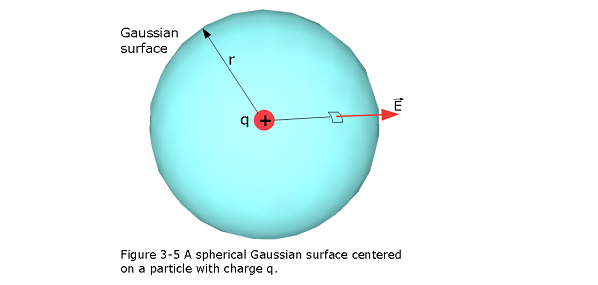
One of the situations in which we can apply Gauss’ law is in finding the electric field of a charged particle. That field has spherical symmetry (the field depends on the distance r from the particle but not the direction). So, to make use of that symmetry, we enclose the particle in a Gaussian sphere that is centered on the particle, as shown in Fig. 3-5 for a particle with positive charge q.Then the electric field has the same magnitude E at any point on the sphere (all points are at the same distance r).That feature will simplify the integration.

From the symmetry of the situation,we know that the electric field \(\vec E\) at the patch is also radially outward and thus at angle \(\theta = 0\) with \(d\vec E\).So, we rewrite Gauss’ law as

\[\begin{equation} \varepsilon_0\oint {\vec E.d\vec A} = \varepsilon_0\oint {EdA} = q_{enc} \tag{3.4} \end{equation}\]

Here \(q_{enc} = q\). Because the field magnitude E is the same at every patch element, E can be pulled outside the integral:

\[\begin{equation} \varepsilon_0E\oint {dA} = q \space\space \tag{3.5} \end{equation}\]

Integration over a sperical surface will give us \(4\pi r^2\) and thus

\[\begin{equation} \varepsilon_0E{(4\pi r^2)} = q \space\space \tag{3.6} \end{equation}\]

The electric field due to a point charge at a radial distance is given by

\[\begin{equation} E = \frac{1}{4\pi \varepsilon_0}\frac{q}{r^2} \tag{3.7} \end{equation}\]

This is exactly Eq. 22-4,which we found using Coulomb’s law.

Example Problem 3-3: Using Gauss’ law to find the electric field Figure 3-6a shows, in cross section, a plastic, spherical shell with uniform charge Q = -16e and radius R = 10 cm. A particle with charge q = +5e is at the center. What is the electric field (magnitude and direction) at (a) point \(P_1\) at radial distance \(r_1\) = 6.00 cm and (b) point \(P_2\) at radial distance \(r_2\) = 12.0 cm?

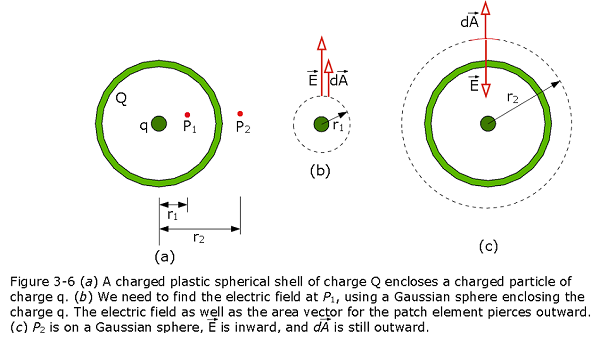
Solution: (a) Using Gauss’s law as given in Eqn. 3-3, we can find out the electric field enclosing the charge q = 5e at a radial distance r = \(r_1 = 6.00\times 10^{-2}\) m, as

\[\varepsilon_0\oint {\vec E.d\vec A} = q_{enc}\] \[\varepsilon_0E\oint dA = q_{enc}\] \[\varepsilon_0E(4\pi r^2) = q_{enc}\] \[E = \frac{1}{4\pi\varepsilon_0}\frac{q_{enc}}{ r^2}=\left({8.99 \times 10^9}{\frac{N.m^2}{C^2}}\right)\frac{5\times 1.6\times 10^{-19}\space C}{(6.00\times 10^{-2}\space m)^2} \approx 2.0\times 10^{-6}\space N/C\space (Answer)\] (b) Again, using Gauss’s law as given in Eqn. 3-3, we can find out the electric field enclosing the charge \(q_{enc} = q + Q = 5e+(-16q)=-11q\) at a radial distance r = \(r_2 = 12.0 \times 10^{-2}\) m, as

\[E = \frac{1}{4\pi\varepsilon_0}\frac{q_{enc}}{ r^2}=\left({8.99 \times 10^9}{\frac{N.m^2}{C^2}}\right)\frac{-11\times 1.6\times 10^{-19}\space C}{(12.00\times 10^{-2}\space m)^2} \approx -1.10\times 10^{-6}\space N/C\space (Answer)\] Example Problem 3-4:

A nonuniform electric field given by \(\vec E = 3.0x\hat i+ 4.0\hat j\) pierces the Gaussian cube shown in Fig. 3-7a. (E is in newtons per coulomb and x is in meters.) What is the electric flux through the right face, the left face, the top face, the bottom face, front face and back face? What is the net charge enclosed by the Gaussian cube?

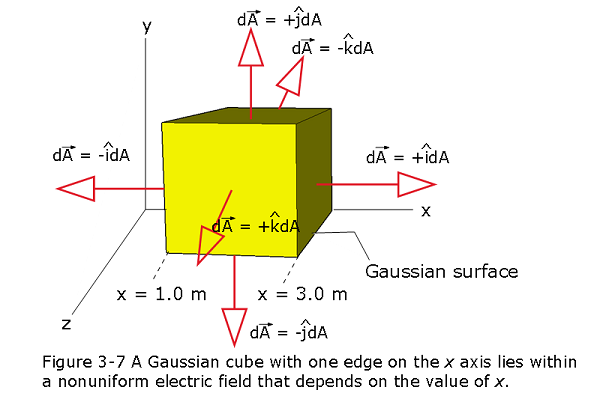
Solution:

\[\Phi_{left}=\int {\vec E.d\vec A}=\int (3.0x\hat i+ 4.0\hat j).(-\hat idA)=-(3.0)(1.0\space m)(4\space)=-12.0\space N-m^2/C \space (Answer)\] \[\Phi_{right}=\int {\vec E.d\vec A}=\int (3.0x\hat i+ 4.0\hat j).(\hat idA)=(3.0)(3.0\space m)(4\space)=36.0\space N-m^2/C \space (Answer)\] \[\Phi_{top}=\int {\vec E.d\vec A}=\int (3.0x\hat i+ 4.0\hat j).(\hat jdA)= 16.0 \space N-m^2/C\space (Answer)\] \[\Phi_{bottom}=\int {\vec E.d\vec A}=\int (3.0x\hat i+ 4.0\hat j).(-\hat jdA)= -16.0 \space N-m^2/C\space (Answer)\] \[\Phi_{front}=\int {\vec E.d\vec A}=\int (3.0x\hat i+ 4.0\hat j).(\hat kdA)= 0 (Answer)\] \[\Phi_{back}=\int {\vec E.d\vec A}=\int (3.0x\hat i+ 4.0\hat j).(-\hat kdA)= 0 (Answer)\] Thus, the net flux is \[\Phi_{net}= \Phi_{left}+\Phi_{right}+\Phi_{top}+\Phi_{bottom}+\Phi_{front}+\Phi_{back}= 12+36+16-16+0+0)n-m^2/C= \] \[\Phi_{net}= (-12+36+16-16+0+0)N-m^2/C=24\space N-m^2/C \] Enclosed charge \[q_{enc}=\varepsilon_0\Phi= (8.85\times10^{-12}\space C^2/N-m^2)(24\space N-m^2/C)= 2.1\times 10 ^{-10}\space C\space (Answer)\]

3.4 A Charged Isolated Conductor:

In Electrostatic at equilibrium the electric field is zero inside a conductor, charges in a Conductor redistribute themselves wherever they are needed to make the field inside the conductor zero.

Faraday’s Cage demonstrates that inside cavity is “shielded” from all external electric fields (see Figure 3-8). A car or airplane with metallic body is an example of a Faraday’s Cage and as a result it is guarded from the lighting strikes.

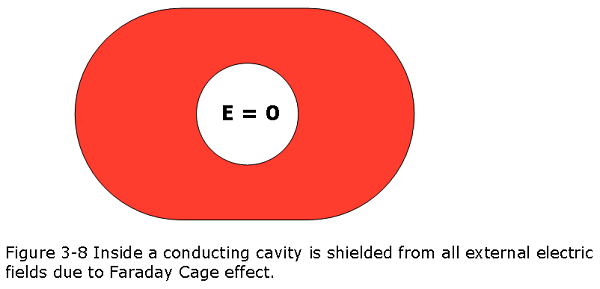
In a given hollow conductor of arbitrary shape, an excess charge Q is placed on the conductor is placed in an external electric field charge inside is 0 and outside it is Q.

Example Problem 3-5:

A spherical conducting shell has an excess charge of +15 C. A point charge of –25 C is located at center of the sphere. Use Gauss’ Law to calculate the charge on inner and outer surfaces of the spherical shell.

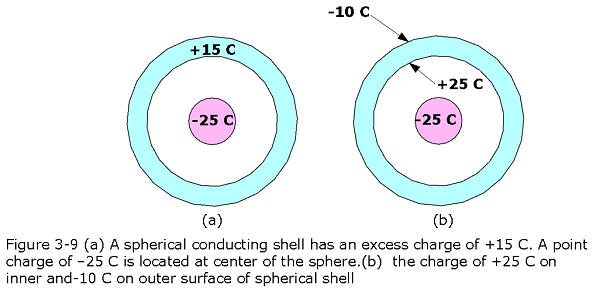
Solution:

Since charge on the outer shell is +15 C, charge on outer surface = +15 C - 25 C = -10 C

Therefore, inner shell +25 C and outer shell –10 C.

3.5 Charges in Conductors

Gauss’ law permits us to prove an important theorem about conductors: Theorem: If an excess charge is placed on an isolated conductor, that amount of charge will move entirely to the surface of the conductor. None of the excess charge will be found within the body of the conductor.

Example Problem 3.06

Spherical metal shell, electric field and enclosed charge Figure 3-10a shows a cross section of a spherical metal shell of inner radius R. A particle with a charge of \(-5.0 \mu\)C is located at a distance R/2 from the center of the shell. If the shell is electrically neutral, what are the (induced) charges on its inner and outer surfaces? Are those charges uniformly distributed? What is the field pattern inside and outside the shell?

Figure 3-10b shows a cross section of a spherical Gaussian surface within the metal, just outside the inner wall of the shell. The electric field must be zero inside the metal (and thus on the Gaussian surface inside the metal). This means that the electric flux through the Gaussian surface must also be zero. Gauss’ law then tells us that the net charge enclosed by the Gaussian surface must be zero.

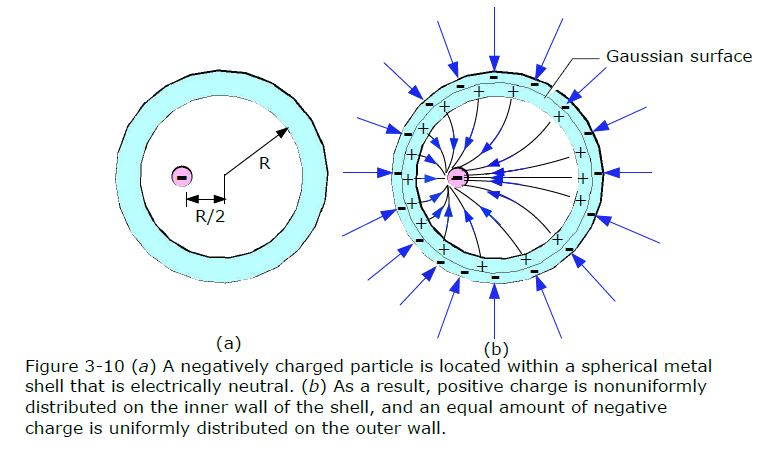
Solution:

Charges will be “induced” in the conductor to make the field inside the conductor zero. With a particle of charge \(-5.0 \mu\)C within the shell, a charge of \(+5.0 \mu\)C must lie on the inner wall of the shell in order that the net enclosed charge be zero. If the particle were centered, this positive charge would be uniformly distributed along the inner wall.

Outside the shell, the field is the same as the field produced by a charge at the center. Because the shell is electrically neutral, its inner wall can have a charge of \(+5.0 \mu\)C only if electrons, with a total charge of \(-5.0 \mu\)C, leave the inner wall and move to the outer wall. There they spread out uniformly, as is also suggested by Fig. 3-10b. This distribution of negative charge is uniform because the shell is spherical and because the skewed distribution of positive charge on the inner wall cannot produce an electric field in the shell to affect the distribution of charge on the outer wall.

3.6 Electric Field of a Conducting Surface:

The surface charge density \(\sigma\) (charge per unit area) over a conducting surface is assumed to be uniform.

Imagine a tiny cylindrical Gaussian surface to be partially embedded in the section as shown in Fig. 3-11, with one end cap is fully inside the conductor, the other is fully outside, and the cylinder is perpendicular to the conductor’s surface.

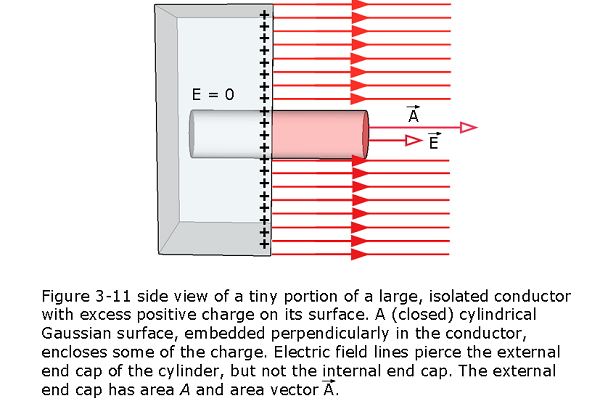
The electric field \(\vec E\) at and just outside the conductor’s surface must also be perpendicular to that surface. If it were not, then it would have a component along the conductor’s surface that would exert forces on the surface charges, causing them to move. However, such motion would violate our implicit assumption that we are dealing with electrostatic equilibrium. Therefore, \(\vec E\) is perpendicular to the conductor’s surface.

The charge \(q_{enc}\) enclosed by the Gaussian surface lies on the conductor’s surface in an area A. If \(\sigma\) is the charge per unit area, then \(q_{enc}\) is equal to \(\sigma A\). When we substitute \(\sigma A\) for \(q_{enc}\) and EA for \(\Phi\), Gauss’ law (Eq. 3-3) becomes

\(\varepsilon_0EA = \sigma A\)

and the electric field on the conducting surface becomes

\[\begin{equation} E = \frac{\sigma}{\varepsilon_0}\space\space (electric~field~on~a~conducting~surface) \tag{3.8} \end{equation}\]

3.7 Applying Gauss’ Law: Cylindrical Symmetry:

Figure 3-12 shows a section of an infinitely long cylindrical non-conducting rod with a uniform charge density \(\lambda\).We want to find an expression for the electric field magnitude E at radius r from the central axis of the rod, outside the rod.

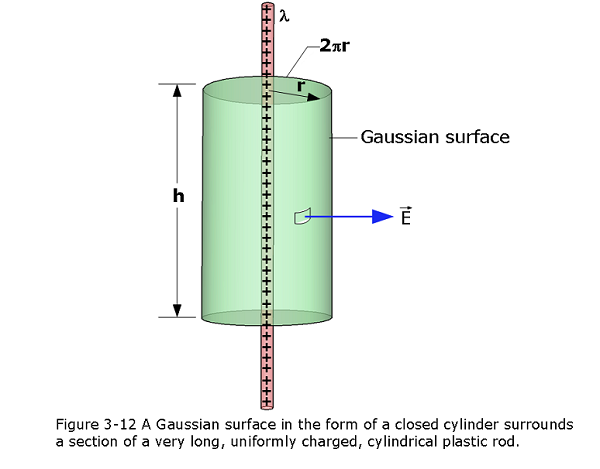
To find the flux through the cylinder’s curved surface, the area vector \(d\vec A\) is radially outward (away from the interior of the Gaussian surface) and thus in the same direction as the field piercing a given patch as shown in Figure 3-12.The dot product in Gauss’ law is then simply \(EdAcos0 = EdA\), and we can pull E out of the integral as given below:

\(\varepsilon_0\oint {\vec E.d\vec A} = \varepsilon_0E\oint {dA}cos\theta = \varepsilon_0EAcos0 = \varepsilon_0E(2\pi rh)\)

\(\varepsilon_0E(2\pi rh) = \lambda h\)

\[\begin{equation} E = \frac{\lambda}{2\pi\varepsilon_0 r} \space\space (Line~of~Charge) \tag{3.9} \end{equation}\]

3.8 Applying Gauss’ Law: Planar Symmetry:

Figure 3-13 shows a portion of a thin, infinite, nonconducting sheet with a uniform (positive) surface charge density \(\sigma\). A useful Gaussian surface is a closed cylinder with end caps of area A, arranged to pierce the sheet perpendicularly as shown in Figure 3-13(b).

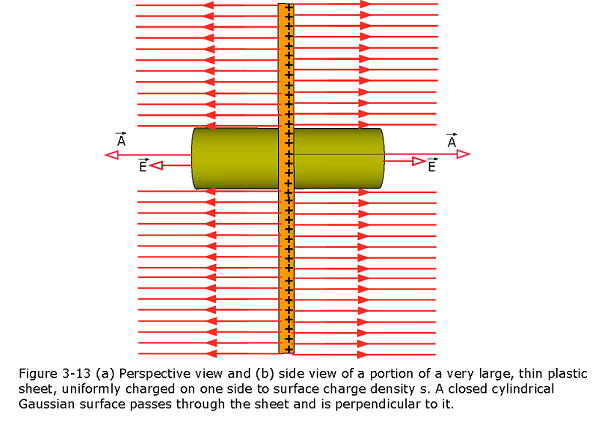
Applying Gauss’ Law we can find the following:

\(\varepsilon_0\oint {\vec E.d\vec A} = q_{enc} \space\space (Gauss'~Law)\)

\(\varepsilon_0 (EA +EA) = \sigma A\)

\[\begin{equation} E = \frac{\sigma}{2\varepsilon_0} \space\space (Sheet~of~Charge) \tag{3.10} \end{equation}\]

3.9 Applying Gauss’ Law: Spherical Symmetry:

A spherical shell of uniform charge attracts or repels a charged particle that is outside the shell as if all the shell’s charge were concentrated at the center of the shell.

Figure 3-14a shows a charged spherical shell of total charge q and radius R and two concentric spherical Gaussian surfaces, \(S_1\) and \(S_2\). Applying Gauss’ law to surface \(S_2\),for which \(r \ge R\),we would find that

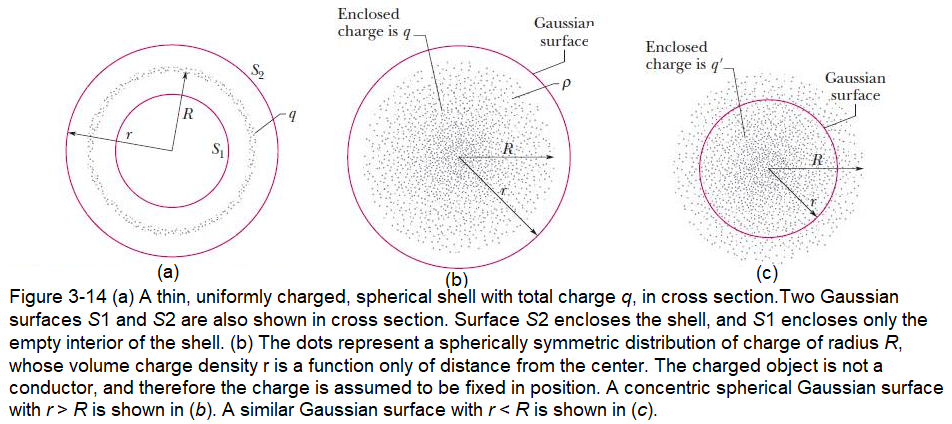
\(\varepsilon_0\oint {\vec E.d\vec A} = q_{enc} \space\space (Gauss'~Law)\)

\(\varepsilon_0E\oint {dA} = q\)

\(\varepsilon_0E{(4\pi r^2)} = q\)

\[\begin{equation} E = \frac{q}{4\pi\varepsilon_0r^2} \space\space (Spherical~Shell~r\ge R) \tag{3.11} \end{equation}\]

Applying Gauss’ law to surface \(S_1\), for which r < R, leads directly to

\[\begin{equation} E = 0 \space\space (Spherical~Shell~r < R) \tag{3.12} \end{equation}\]

If a charged particle is located inside a shell of uniform charge, there is no electrostatic force on the particle from the shell.

Any spherically symmetric charge distribution, such as that of Fig. 3-14, can have two two situations. In Fig. 3-14b, the entire charge lies within a Gaussian surface with r > R and in Figure 3-14b shows a Gaussian surface with r < R.

In Fig. 3-14b, the entire charge lies within a Gaussian surface with r > R. The charge produces an electric field on the Gaussian surface as if the charge were that of a particle located at the center, and the electric field is given by Eq. 3-11:

\[\begin{equation} E = \frac{q}{4\pi\varepsilon_0r^2} \space\space (Spherical~Shell~r\ge R) \tag{3.11} \end{equation}\]

Figure 3-14c shows a Gaussian surface with r < R. To find the electric field at points on this Gaussian surface, we separately consider the charge inside it and the charge outside it. The inside charge sets up a field as though it is concentrated at the center. Letting q’ represent that enclosed charge, we can then rewrite Eq. 3-11 as

\[\begin{equation} E = \frac{q'}{4\pi\varepsilon_0r^2} \space\space (Spherical~distribution,~field~at~r\le R) \tag{3.13} \end{equation}\]

If the full charge q enclosed within radius R is uniform, then q’ enclosed within radius r in Fig. 3-14c is proportional to q:

\[\begin{equation} \frac{q'}{\frac{4}{3}\pi r^3} = \frac{q}{\frac{4}{3}\pi R^3} \tag{3.14} \end{equation}\]

This leads to

\[\begin{equation} q' = q \frac{r^3}{R^3} \tag{3.15} \end{equation}\]

Substituting Eq. 3-15 in Eq. 3-13, we can get the electric field inside \(r \le R\)

\[\begin{equation} E = \left(\frac {q}{4\pi\varepsilon_0 R^3}\right) r\space\space\space (uniform~charge,~field~at~ r\le R). \tag{3.16} \end{equation}\]

Solved Problems Gauss-Law

1. [2] An electric field given by \(\vec E = 4.0\hat i-3.0(y^2+2.0)\hat j\) pierces a Gaussian cube of edge length 2.0 m and positioned as shown in Fig. 3-7. (The magnitude E is in newtons per coulomb and the position x is in meters.) What is the electric flux through the (a) top face, (b) bottom face, (c) left face, and (d) back face? (e) What is the net electric flux through the cube?

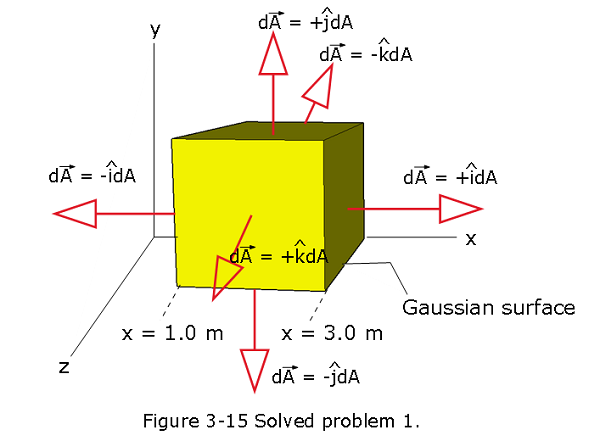
Solution:

1. The electric flux through the top face where y = 2.0 m

\[\Phi_{top} = \int {\vec E.d\vec A}=\int (4.0\hat i-3.0(y^2+2.0)\hat j).(\hat j dA)\] \[\Phi_{top} = \int (4.0\hat i-3.0((2~m)^2+2.0)\hat j).(\hat j dA)\] \[\Phi_{top}=(-18)(4~m^2)= -72~N.m^2/C~(Answer)\] (b) The electric flux through the bottom face where y = 2.0 m \[\Phi_{bottom} = \int (4.0\hat i-3.0((0)^2+2.0)\hat j).(-\hat j dA)=+24~N.m^2/C~(Answer)\] (c) The electric flux through the left face

\[\Phi_{left} = \int {\vec E.d\vec A}=\int (4.0\hat i-3.0(y^2+2.0)\hat j).(-\hat i dA)=-16~N.m^2/C~(Answer)\] (d) The electric flux through the back face

\[\Phi_{back} = \int {\vec E.d\vec A}=\int (4.0\hat i-3.0(y^2+2.0)\hat j).(-\hat k dA)= 0~(Answer)\] (e) The net electric flux through the cube

\[\Phi_{net} = \Phi_{top}+\Phi_{bottom}+\Phi_{left}+\Phi_{right}+\Phi_{front}+\Phi_{back}\] \[\Phi_{net} =(-72+24-16+16+0+0)=-48~N.m^2/C~(Answer)\]

2. [5] In Fig. 3-16, a proton is a distance d/2 directly above the center of a square of side d. What is the magnitude of the electric flux through the square? (Hint:Think of the square as one face of a cube with edge d.)

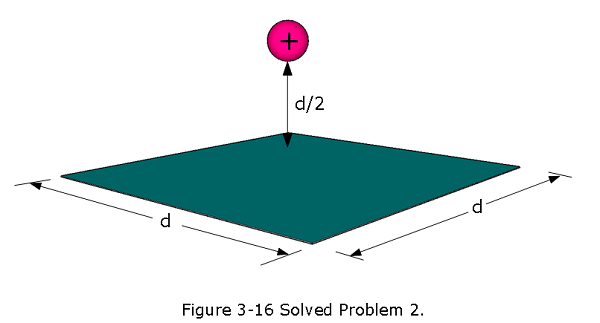
Solution:

A proton is placed at the center of a cube and the total flux through the cube is \(\Phi_{total}= \frac{q}{\epsilon_0}\). Given square is just one of the six faces a cube has and as a result the flux through is one sixth of the total flux.

\(\Phi_{square}= \frac{q}{6\epsilon_0}=\frac{1.6\times 10^{-19}~C}{6\times (8.85\times 10^{-12}~C^2/N.m^2)} = 3.01\times 10^{-9}~\frac{N.m^2}{C}~(Answer)\)

3. [9] Fig. 3-17 shows a Gaussian surface in the shape of a cube with edge length 1.40 m.What are (a) the net flux \(\Phi\) through the surface and (b) the net charge \(q_{enc}\) enclosed by the surface if \(\vec E = (3.00y\hat j)\space N/C\) with y in meters? What are (c) \(\Phi\) and (d) \(q_{enc}\) if \(\vec E = -4.00\hat i+(6.00 + 3.00 y)\hat j\space N/C?\)

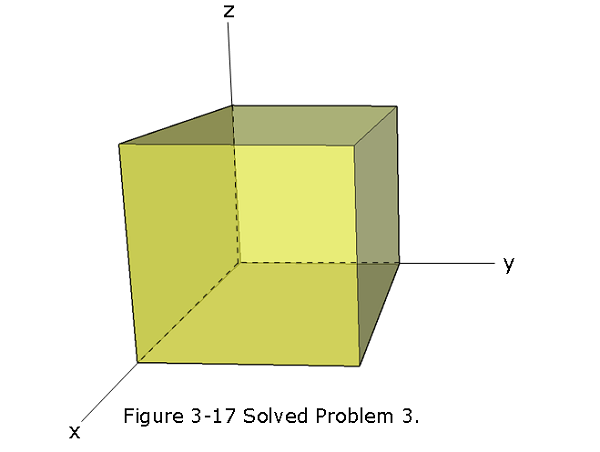
Solution:

1. Flux is going to be contributed only along the y-axis since electric field is aligned along the y-axis. No flux is going to be contributed from the x and z-axis.

\[\Phi_{net} = \oint {\vec E.d\vec A}=\int {(3.00~N/C)(1.40~m)\hat j.(\hat j dA)}-\int {(3.00~N/C)(0)\hat j.(-\hat j dA)}\] \[\Phi_{net} = \int {(3.00~N/C)(1.40~m)\hat j.(\hat j dA)}-0=(3.00~N/C)(1.40~m)^3=8.232~\frac{N.m^2}{C}~(Answer)\] (b) The net charge \(q_{enc}\) enclosed by the surface

\[q_{enc}=\Phi_{net}{\varepsilon_0}=(8.232~\frac{N.m^2}{C})\left(8.85\times 10^{-12}~\frac{C^2}{N.m^2}\right)=7.29\times 10^{-11}~C~(Answer) \] (c) \[\Phi_{net} = \oint {\vec E.d\vec A}=-4.00\hat i+(6.00 + 3.00 y\hat j).d\vec A=(-4.00\hat i).(\hat i dA))+(-4.00\hat i).(-\hat i dA))+(6.00 + 3.00 y\hat j).(\hat j dA)+(6.00 + 3.00 y\hat j).(-\hat j dA)\] \[\Phi_{net} =\int (-4.00\hat i).(\hat i dA))+\int (-4.00\hat i).(-\hat i dA))+\int (6.00 + 3.00 y\hat j).(\hat j dA)+(6.00 + \int 3.00 y\hat j).(-\hat j dA)\] \[\Phi_{net} = \int (6.00 + 3.00 y)\hat j.(\hat j dA)+\int (6.00 + 3.00 y)\hat j.(-\hat j dA)\] \[\Phi_{net} =3.00(1.4~m)(1.4~m)^2+3.00(0)(1.4~m)^2=8.232~\frac{N.m^2}{C}~(Answer)\] (d) \[q_{enc}=\Phi_{net}{\varepsilon_0}=(8.232~\frac{N.m^2}{C})\left(8.85\times 10^{-12}~\frac{C^2}{N.m^2}\right)=7.29\times 10^{-11}~C~(Answer) \]

4. [10] Figure 3-18 shows a closed Gaussian surface in the shape of a cube of edge length 2.00 m. It lies in a region where the nonuniform electric field is given by \(\vec E = (3.00x + 4.00)\hat i+[6.00\hat j+7.00\hat k\space ]N/C\) with x in meters. What is the net charge contained by the cube?

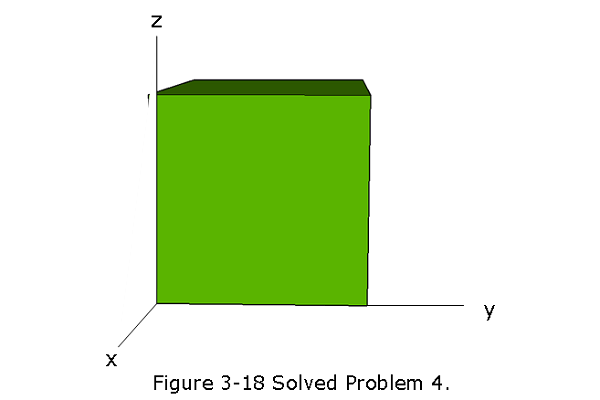
Solution:

The constant terms of the electric fields will cancel each other and contribute nothing to the result. So, we may simplify the electric electric containing only x-dependent component \(\vec E = (3.00x)\hat i\). The net flux is then

\[\Phi_{net} = \int (3.00x)\hat i.(\hat i dA)+\int (3.00x)\hat i.(-\hat i dA)\] \[\Phi_{net} = (3.00)(2.0~m)(2.0~m)^2+(3.00)(0)(2.0~m)^2=24~\frac{N.m^2}{C}\]

\[q_{enc}=\Phi_{net}{\varepsilon_0}=(24~\frac{N.m^2}{C})\left(8.85\times 10^{-12}~\frac{C^2}{N.m^2}\right)=2.12\times 10^{-10}~C~(Answer) \]

5. [14] Flux and nonconducting shells. A charged particle is suspended at the center of two concentric spherical shells that are very thin and made of nonconducting material. Figure 3-19a shows a cross section. Figure 3-19b gives the net flux \(\Phi\) through a Gaussian sphere centered on the particle, as a function of the radius r of the sphere. The scale of the vertical axis is set by \(\Phi_s = 5.0\times 10^5\space N.m^2/C\). (a) What is the charge of the central particle? What are the net charges of (b) shell A and (c) shell B?

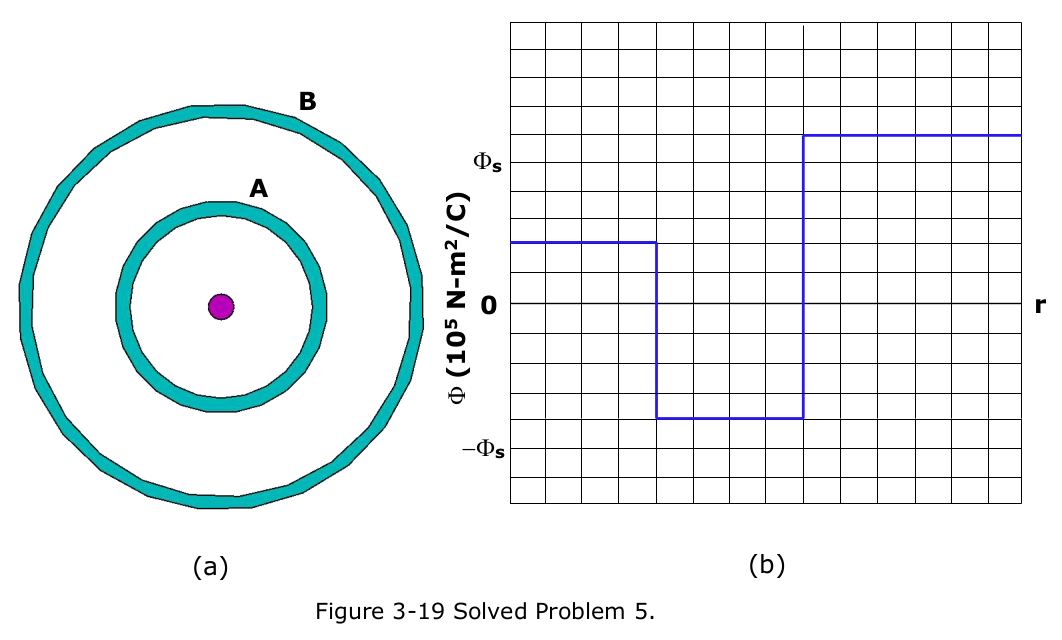
Solution:

1. Charge of the central particle: \[\Phi= 2 \times 10^5\space N.m^2/C\] \[q_{central}=\Phi{\varepsilon_0}=\left (2\times 10^5~\frac{N.m^2}{C}\right)\left(8.85\times 10^{-12}~\frac{C^2}{N.m^2}\right)=1.77\times 10^{-6}~C~(Answer) \]

2. Net charge of shell A: \[q_{Shell-A}=\Phi{\varepsilon_0}-1.77\times 10^{-6}~C\] \[q_{Shell-A}=\left (-4\times 10^5~\frac{N.m^2}{C}\right)\left(8.85\times 10^{-12}~\frac{C^2}{N.m^2}\right)-1.77\times 10^{-6}~C\] \[q_{Shell-A}=- 3.54\times 10^{-6}~C-1.77\times 10^{-6}~C =-5.31\times 10^{-6}~C~(Answer)\]

3. Net charge of shell B:

\[q_{Shell-B}=\Phi{\varepsilon_0}-q_A-q_{central}\] \[q_{Shell-B}=\left (6\times 10^5~\frac{N.m^2}{C}\right)\left(8.85\times 10^{-12}~\frac{C^2}{N.m^2}\right)-q_A-q_{central}\] \[q_{Shell-B}=5.31\times 10^{-6}~C-(-5.31\times 10^{-6}~C)-1.77\times 10^{-6}~C=8.85\times 10^{-6}~C~(Answer)\]

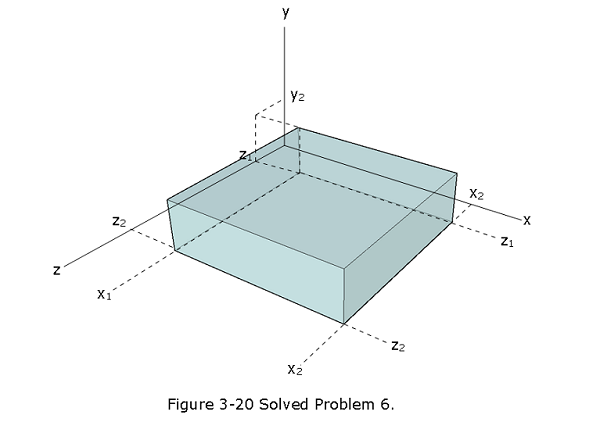
6. [16] The box-like Gaussian surface shown in Fig. 3-20 encloses a net charge of \(+24.00\varepsilon_0\space C\) and lies in an electric field given by \(\vec E = [(10.0 + 2x)\hat i-3.0\hat j+bz\hat k]\space N/C\) with x and z in meters and b a constant. The bottom face is in the xz plane; the top face is in the horizontal plane passing through \(y_2 = 1.00\) m. For \(x_1 = 1.00\) m, \(x_2 = 4.00\) m, \(z_1 = 1.00\) m, and \(z_2 = 3.00\) m, what is b?

Solution:

\[\Phi_{net} = \oint {\vec E.d\vec A}=\frac{q_{enc}}{\epsilon_0}=\frac{+24.00\varepsilon_0\space C}{\epsilon_0}=24\space N.m^2/C\] \[\Phi_{net} =\Phi_{x}+\Phi_{y}+\Phi_{z}\] \[\Phi_{x}=\int {\vec E.d\vec A}=E_x(x_2)A_{yz}-E_x(x_1)A_{yz}=(10+2x_2)A_{yz}-(10+2x_1)A_{yz}\] Substituting \(A_{yz}=y_2(z_2-z_1)\), we get

\[\Phi_{x}=(10+2x_2)A_{yz}-(10+2x_1)A_{yz}=2y_2(z_2-Z1)(x_2-x_1)=2(1)(2)(3)= 12\space N.m^2/C\] \[\Phi_{y}=\int {\vec E.d\vec A}= E_yA_{xz}-E_yA_{xz}=0\] \[\Phi_{z}=\int {\vec E.d\vec A}=E_z(z_2)A_{xy}-E_z(z_1)A_{xy}=bz_2A_{xy}-bz_1A_{xy}\] Substituting, \(A_{xy}=y_2(x_2-x_1)\), we get \[\Phi_{z} = by_2(x_2-x_1)(z_2-z_1)=b(1)(3)(2) = 6b\] \[\Phi_{net} =\Phi_{x}+\Phi_{y}+\Phi_{z}=12+0+6b=24\] \[b=2~N.m/C~(Answer)\]

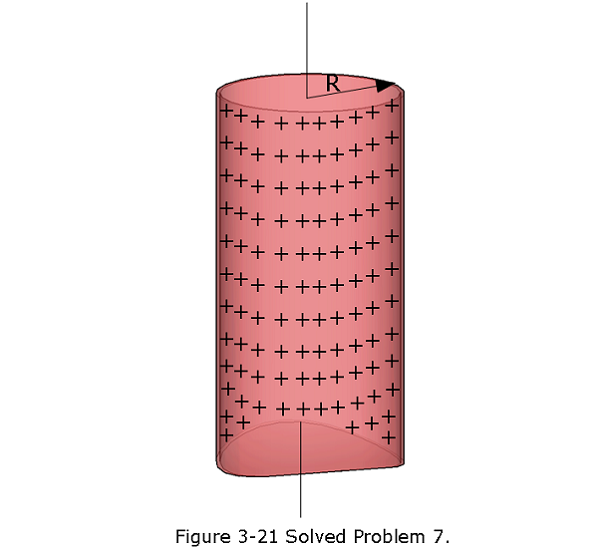
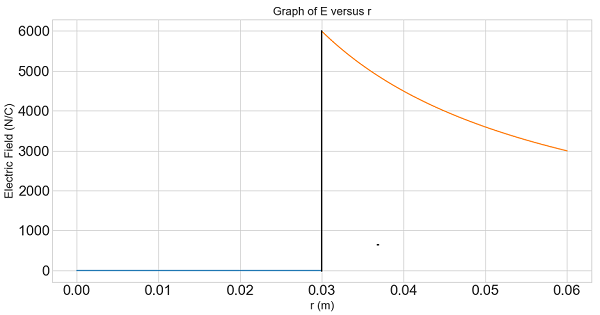
7. [24] Figure 3-21 shows a section of a long, thin-walled metal tube of radius R = 3.00 cm, with a charge per unit length of \(\lambda = 2.00 \times 10^{-8}\) C/m. What is the magnitude E of the electric field at radial distance (a) r = R/2.00 and (b) r = 2.00R? (c) Graph E versus r for the range r = 0 to 2.00R.

Solution:

1. To calculate the electric field with a cylindrical symmetry we can apply \(\varepsilon_0\oint \vec E.d\vec A =q_{enc}\) in an immaginary Gaussian cylinder of radius r = R/2.00 = 1.50 cm. We get, \[E = \frac{q_{enc}}{\varepsilon_0L2\pi r }\], where area of the immaginary Gaussian cylinder is \(A = 2\pi r L\), L is the length of the cylinder. At r = R/2.00 = 1.50 cm, there is no net enclosed charge, \(q_{enc} = 0\). Therefore, \[E(r = 1.5 cm, r < R) = 0~(Answer)\]
2. Electric field at r = 2.00R, \[E = \frac{q_{enc}}{\varepsilon_0L2\pi 2R}= \frac{\lambda L}{\varepsilon_0L2\pi 2R}=\frac{\lambda}{4\pi\varepsilon_0 R}\]

\[E = \frac{\lambda}{4\pi\varepsilon_0 R}=\left({8.99 \times 10^9}{\frac{N.m^2}{C^2}}\right)\frac{2.00 \times 10^{-8}~ C/m}{3.00\times 10^{-2}~m}= 5.99\times 10^{3}~N/C~(Answer)\] (c) Graph E versus r for the range r = 0 to 2.00R.

8. [28] A charge of uniform linear density 2.0 nC/m is distributed along a long, thin, nonconducting rod. The rod is coaxial with a long conducting cylindrical shell (inner radius = 5.0 cm, outer radius = 10 cm). The net charge on the shell is zero. (a) What is the magnitude of the electric field 15 cm from the axis of the shell? What is the surface charge density on the (b) inner and (c) outer surface of the shell?

Solution:

1. The magnitude of the electric field 15 cm from the axis of the shell can be found by using Eq. 3-9, \[E = \frac{\lambda}{2\pi\varepsilon_0 r}=\frac{2\times 10^{-9}~C/m}{2\pi(8.85\times 10^{-12}\frac{C^2}{N.m^2}) (0.15~m)}=239.7~N/C\approx 240~N/C~(Answer)\]
2. Surface charge density on the inner surface of the shell.

\[\sigma = \frac{-q}{A}=\frac{-q}{2\pi r_i L}=\frac{-\lambda L}{2\pi r_i L}=\frac{-\lambda}{2\pi r_i}=\frac{-2.0\times 10^{-9}~C/m}{2\pi (0.05~m)}= -6.37\times 10^{-9}~C/m^2~(Answer)\]

3. Surface charge density on the outer surface of the shell. \[\sigma = \frac{\lambda}{2\pi r_o}=\frac{-2.0\times 10^{-9}~C/m}{2\pi (0.10~m)}= 3.18\times 10^{-9}~C/m^2~(Answer)\]

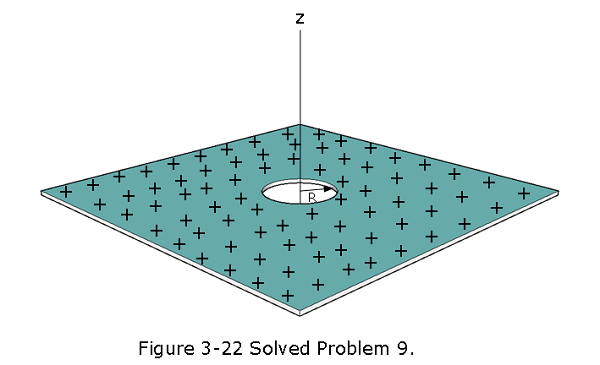
9. [34] In Fig. 3-22, a small circular hole of radius R = 1.80 cm has been cut in the middle of an infinite, flat, nonconducting surface that has uniform charge density \(\sigma = 4.50 \space pC/m^2\). A z axis, with its origin at the hole’s center, is perpendicular to the surface. In unit vector notation, what is the electric field at point P at z = 2.56 cm? (Hint: See Eq. 2-23 and use superposition.)

Solution:

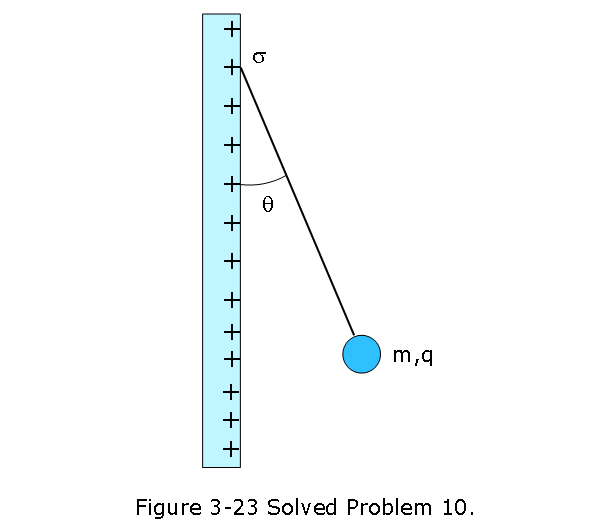
\[E_{net}=E_{sur}-E_{disk}=\frac{\sigma}{2\varepsilon_0}-\frac{\sigma}{2\varepsilon_{0}}\left[1-\frac{z}{\sqrt{z^2 + R^2}}\right]=\frac{\sigma}{2\varepsilon_0}\frac{z}{\sqrt{z^2 + R^2}}\] \[E_{net} = \frac{4.50 \times 10^{12}\space C/m^2}{2\times8.85\times 10^{-12}~C^2/N.m^2 }\frac{0.0256~m}{\sqrt{(0.0256~m)^2 + (0.018~m)^2}}=0.208~N/C~(Answer)\] 10. [39] In Fig. 3-23, a small, nonconducting ball of mass m = 1.0 mg and charge q \(2.0 \times 10^{-8}\) C (distributed uniformly through its volume) hangs from an insulating thread that makes an angle \(\theta = 30^\circ\) with a vertical, uniformly charged nonconducting sheet (shown in cross section). Considering the gravitational force on the ball and assuming the sheet extends far vertically and into and out of the page, calculate the surface charge density s of the sheet.

Solution:

To solve the prolem, let’s redraw Figure 3-23, showing the free-body diagram to resolve the forces along the x and y-axes.

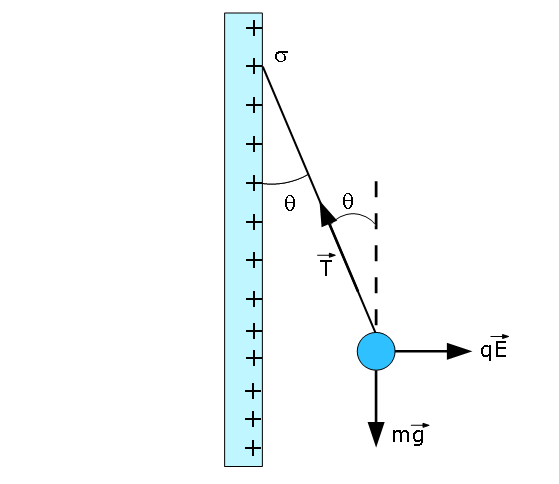
We get following two equations, along the x and y-axes.

\[qE -T\sin\theta = 0\] \[T\cos\theta -mg = 0\] Diving the above equations we get, \(\tan\theta=\frac{qE}{mg}\). Substituting \(E = \frac{\sigma}{2\varepsilon_0}\) for a uniformly charged nonconducting sheet, we get

\[\sigma = \frac{2mg\tan\theta\varepsilon_0}{q}=\frac{2(1.0\times 10^{-3}~kg)(9.8~m/s^2)\tan30^\circ(8.85\times 10^{-12}~C^2/N.m^2)}{2.0 \times 10^{-8}~C}\] \[=5.0\times 10^{-9}~C/m^2~(Answer)\] 11. [49] In Fig. 3-24, a solid sphere of radius a = 2.00 cm is concentric with a spherical conducting shell of inner radius b = 2.00a and outer radius c = 2.40a. The sphere has a net uniform charge \(q_1 = +5.00\) fC; the shell has a net charge \(q_2 = -q_1\). What is the magnitude of the electric field at radial distances (a) r = 0, (b) r = a/2.00, (c) r = a, (d) r = 1.50a, (e) r = 2.30a, and (f) r = 3.50a? What is the net charge on the (g) inner and (h) outer surface of the shell?

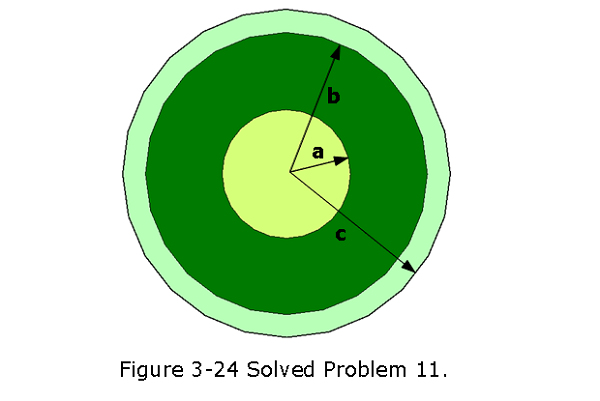
Solution:

Electric field inside the conducting sphere is given by Eq. 3-16, \[E(r) = \left(\frac {q}{4\pi\varepsilon_0 a^3}\right) r\] (a) At r = 0, E(r=0) = 0 (Answer) (b) At r = a/2.00 = 2.00 cm/2.00 = 1 cm, \[E(r) = \left(\frac {1}{4\pi\varepsilon_0}\right) \frac{qr}{a^3}\] \[E(r=0.5a) =\left({8.99 \times 10^9}{\frac{N.m^2}{C^2}}\right)\frac{(5.0\times 10^{-15}~C)}{2(2.0\times 10^{-2}~m)^2}=0.0563~N/C~(Answer)\] (c) At r = a, \[E(r=a) =\left({8.99 \times 10^9}{\frac{N.m^2}{C^2}}\right)\frac{(5.0\times 10^{-15}~C)}{(2.0\times 10^{-2}~m)^2}=0.1125~N/C~(Answer)\]

4. At r = 1.5a, \[E(r=1.5a) =\frac{q_i}{4\pi\varepsilon_0 r^2}=\left({8.99 \times 10^9}{\frac{N.m^2}{C^2}}\right)\frac{(5.0\times 10^{-15}~C)}{(1.5\times 2.0\times 10^{-2}~m)^2}=0.0499~N/C~(Answer)\]

5. At r = 2.30a, b < r < c, \[E(r=2.30a) = 0 ~(Answer)\]

6. At r = 3.50a, r > c, \[E(r=3.5a) = 0(Answer)\]

7. Net charge on the inner surface of the shell is \(q_i\), then \(q_1 + q_i = 0\) and \(q_i = –q_1 = –5.00 \times 10^{-15}~C~(Answer)\).

8. Net charge on the outer surface of the shell, \(q_i + q_o = –q_1\).

\[q_o = –q_1 – q_i = –q_1 –(–q_1) = 0~(Answer)\].

Problems Gauss-Law

Section 3-1 Electric Flux

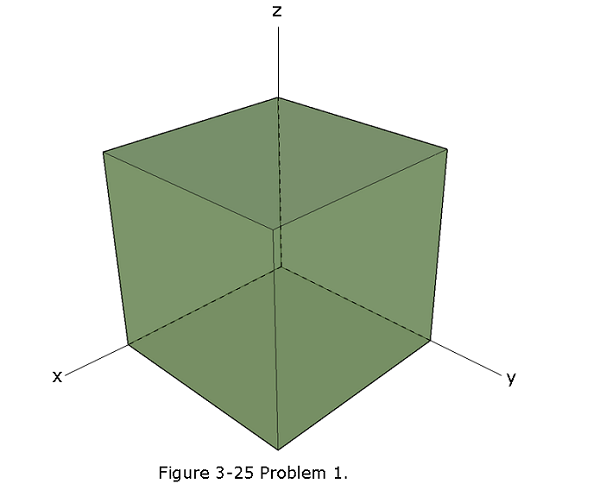
1. [3] The cube in Fig. 3-25 has edge length 1.40 m and is oriented as shown in a region of uniform electric field. Find the electric flux through the right face if the electric field, in newtons per coulomb, is given by (a) \(6.00\hat i\) (b) \(-2.00\hat j\) and (c) \(-3.00\hat i+4.00\hat k\) (d) What is the total flux through the cube for each field?

Section 3-1 Gauss’ Law

2. [6] At each point on the surface of the cube shown in Fig. 3-24, the electric field is parallel to the z axis. The length of each edge of the cube is 3.0 m. On the top face of the cube the field is \(-34\hat k\space N?C\) and on the bottom face it is \(+20\hat k\space N/C\). Determine the net charge contained within the cube.

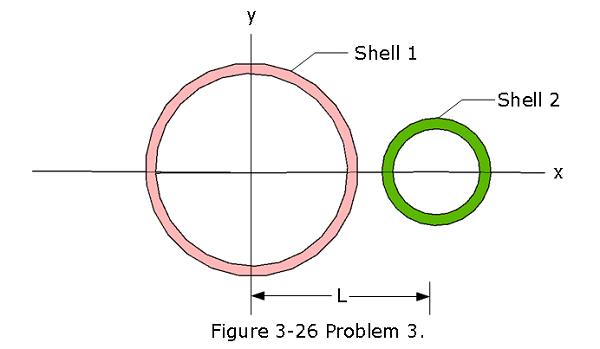
3. [12] Figure 3-26 shows two nonconducting spherical shells fixed in place. Shell 1 has uniform surface charge density \(6.0 \space\mu C/m^2\) on its outer surface and radius 3.0 cm; shell 2 has uniform surface charge density \(4.0 \space\mu C/m^2\) on its outer surface and radius 2.0 cm; the shell centers are separated by L = 10 cm. In unit-vector notation, what is the net electric field at x = 2.0 cm?

4. [15] A particle of charge +q is placed at one corner of a Gaussian cube. What multiple of \(\frac{q}{\varepsilon_0}\) gives the flux through (a) each cube face forming that corner and (b) each of the other cube faces?

Section 3-3 A Charged Isolated Conductor

5. [19] Space vehicles traveling through Earth’s radiation belts can intercept a significant number of electrons. The resulting charge buildup can damage electronic components and disrupt operations. Suppose a spherical metal satellite 1.3 m in diameter accumulates 2.4 mC of charge in one orbital revolution. (a) Find the resulting surface charge density. (b) Calculate the magnitude of the electric field just outside the surface of the satellite, due to the surface charge.

6. [21] An isolated conductor has net charge \(+10 \times 10^{-6}\) C and a cavity with a particle of charge \(q = +3.0 \times 10^{-6}\) C.What is the charge on (a) the cavity wall and (b) the outer surface?

Section 3-4 Applying Gauss’ Law: Cylindrical Symmetry__

7. [23] (a) The drum of a photocopying machine has a length of 42 cm and a diameter of 12 cm.The electric field just above the drum’s surface is \(2.3 \times 10^5\) N/C.What is the total charge on the drum? (b) The manufacturer wishes to produce a desktop version of the machine. This requires reducing the drum length to 28 cm and the diameter to 8.0 cm.The electric field at the drum surface must not change. What must be the charge on this new drum?

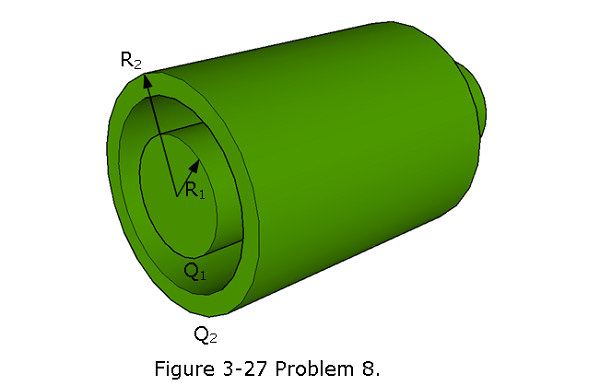
8. [29] Figure 3-27 is a section of a conducting rod of radius \(R_1 = 1.30\) mm and length L = 11.00 m inside a thin-walled coaxial conducting cylindrical shell of radius \(R_2 = 10.0R_1\) and the (same) length L. The net charge on the rod is \(Q_1 = +3.40 \times 10^{-12}\) C; that on the shell is \(Q_2 = -2.00Q_1\). What are the (a) magnitude E and (b) direction (radially inward or outward) of the electric field at radial distance \(r = 2.00R_2\)? What are (c) E and (d) the direction at \(r = 5.00R_1\)? What is the charge on the (e) interior and (f) exterior surface of the shell?

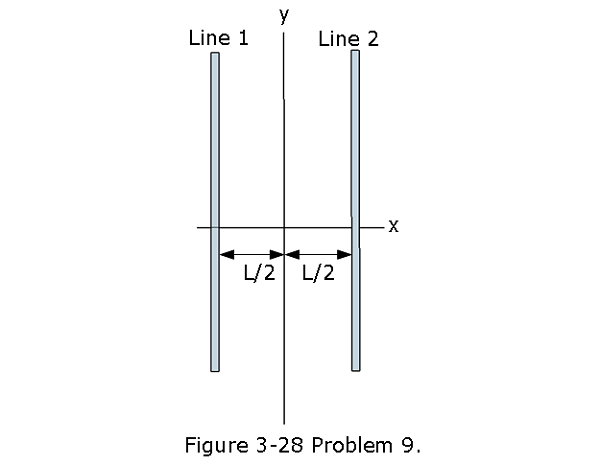
9. [30] In Fig. 3-28, short sections of two very long parallel lines of charge are shown, fixed in place, separated by L = 8.0 cm. The uniform linear charge densities are \(6.0 \space \mu C/m\) for line 1 and \(2.0\space\mu C/m\) for line 2.Where along the x axis shown is the net electric field from the two lines zero?

Module 3-5 Applying Gauss’ Law: Planar Symmetry

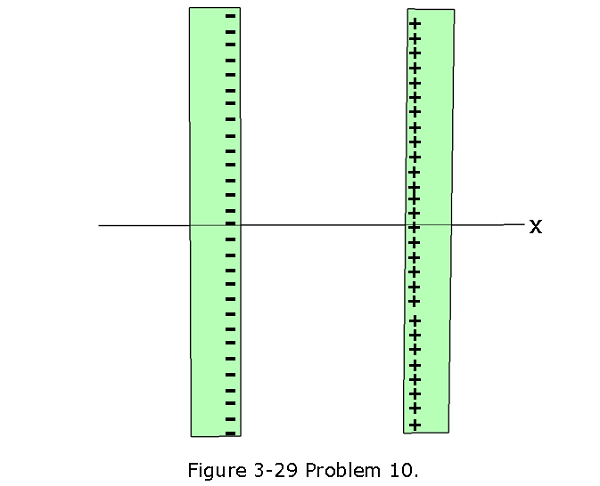
10. [33] In Fig. 3-29, two large, thin metal plates are parallel and close to each other. On their inner faces, the plates have excess surface charge densities of opposite signs and magnitude \(7.00 \times 10^{-22}\space C/m^2\). In unit-vector notation, what is the electric field at points (a) to the left of the plates, (b) to the right of them, and (c) between them?

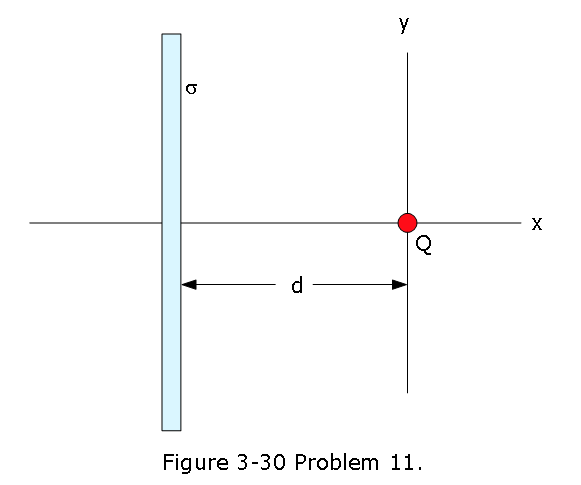
11. [40] Figure 3-30 shows a very large nonconducting sheet that has a uniform surface charge density of \(\sigma = -2.00 \space \mu C/m^2\); it also shows a particle of charge \(Q = 6.00\space \mu C\), at distance d from the sheet. Both are fixed in place. If d = 0.200 m, at what (a) positive and (b) negative coordinate on the x axis (other than infinity) is the net electric field \(\vec E_{net}\) of the sheet and particle zero? (c) If d = 0.800 m, at what coordinate on the x axis \(\vec E_{net}\) = 0?