Appendix-A
Geometry
Circle of radius r: circumference \(2\pi r\); area \(\pi r^2\).
Sphere of radius r: area \(4\pi r^2\) ; \(volume =\frac {4}{3}\pi r^3\) Right circular cylinder of radius r and height h: area = \(2\pi r^2 + 2\pi r h; volume = \pi r^2 h\) Triangle of base a and altitude h: area = \(\frac{1}{2}ah\)
Quadratic Formula
If \(ax^2+bx+c =0\), the roots are \(x = \frac{-b \pm \sqrt{b^2-4ac}}{2a}\)
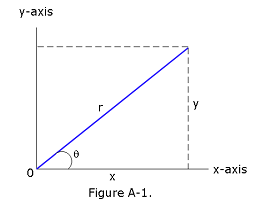
Trigonometric Functions of Angle \(\theta\)
\(\sin\theta=\frac{y}{r}\) \(~~~\cos\theta=\frac{x}{r}\)
\(\tan\theta=\frac{y}{x}\) \(~~~\cot\theta=\frac{x}{y}\)
\(\sec\theta=\frac{r}{x}\) \(~~~\csc\theta=\frac{r}{y}\)
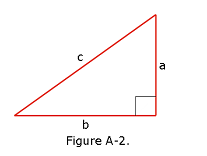
Pythagorean Theorem
In this right triangle,
\(a^2+ b^2 = c^2\)
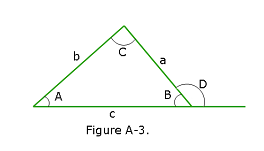
Triangles
Angles are A, B, C Opposite sides are a, b, c Angles \(A + B + C = 180^0\)
\(\frac{\sin A}{a}=\frac{\sin B}{b}=\frac{\sin C}{c}\)
\(c^2 = a^2+b^2-2ab\cos c\)
\(Exterior angle: D =A+C\)
Mathematical Signs and Symbols
Here are some commonly used signs and symbols in mathematics and statistics:
x equals y: \(x = y\)
x is less than y: \(x < y\)
x is greater than y: \(x > y\)
x is less than or equal to y: \(x \leq y\)
x is greater than or equal to y: \(x \geq y\)
x is not equal to y: \(x \neq y\)
x is approximately equal to y: \(x\approx y\)
x is proportional to y: \(x\propto y\)
x to the power n: \(x^{n}\)
x subscript n: \(x_{n}\)
x bar: \(\bar{x}\)
x hat: \(\hat{x}\)
a division b: \(\frac{a}{b}\)
x is a proper subset of y: \(x\subset y\)
x is not a proper subset of y: \(x\not\subset y\)
x is a subset of y: \(x\subseteq y\)
x is not a subset of y: \(x\nsubseteq y\)
X∼Normal(μ,σ) \(X \sim \text{Normal}(\mu, \sigma)\)
Trigonometric Identities
\(\sin\theta=1/\csc\theta\)
\(\cos\theta=1/\sec\theta\)
\(\tan\theta=1/\cot\theta\)
\(\sin(90^{\circ}-\theta)=\cos\theta\)
\(\cos(90^{\circ}-\theta)=\sin\theta\)
\(\tan(90^{\circ}-\theta)=\cot\theta\)
\(\sin^2\theta+\cos^2\theta=1\)
\(\sec^2\theta-\tan^2\theta=1\)
\(\tan\theta=\sin\theta/\cos\theta\)
\(\sin(\alpha\pm\beta)=\sin\alpha\cos\beta\pm\cos\alpha\sin\beta\)
\(\cos(\alpha\pm\beta)=\cos\alpha\cos\beta\mp\sin\alpha\sin\beta\)
\(\tan(\alpha\pm\beta)=\frac{\tan\alpha\pm\tan\beta}{1\mp\tan\alpha\tan\beta}\)
\(\sin2\theta=2\sin\theta\cos\theta\)
\(\cos2\theta=\cos^2\theta-\sin^2\theta=2\cos^2\theta-1\)
\(\cos2\theta=\cos^2\theta-\sin^2\theta=1-2\sin^2\theta\)
\(\sin\alpha+\sin\beta=2\sin\frac{1}{2}(\alpha+\beta)\cos\frac{1}{2}(\alpha-\beta)\)
\(\cos\alpha+\cos\beta=2\cos\frac{1}{2}(\alpha+\beta)\cos\frac{1}{2}(\alpha-\beta)\)
Derivatives
\(\frac{d}{dx}[af(x)]=a\frac{d}{dx}f(x)\)
\(\frac{d}{dx}[f(x)+g(x)]=\frac{d}{dx}f(x)+\frac{d}{dx}g(x)\)
\(\frac{d}{dx}[f(x)g(x)]=f(x)\frac{d}{dx}g(x)+g(x)\frac{d}{dx}f(x)\)
\(\frac{d}{dx}f(u)=\left[\frac{d}{du}f(u)\right]\frac{du}{dx}\)
\(\frac{d}{dx}x^m=mx^{m-1}\)
\(\frac{d}{dx}\sin x=\cos x\)
\(\frac{d}{dx}\cos x=-\sin x\)
\(\frac{d}{dx}\tan x=\sec^2x\)
\(\frac{d}{dx}\cot x=-\csc^2x\)
\(\frac{d}{dx}\sec x=\tan x\sec x\)
\(\frac{d}{dx}\csc x=-\cot x\csc x\)
\(\frac{d}{dx}e^x=e^x\)
\(\frac{d}{dx}\ln x=\frac{1}{x}\)
\(\frac{d}{dx}\sin^{-1}x=\frac{1}{\sqrt{1-x^2}}\)
\(\frac{d}{dx}\cos^{-1}x=-\frac{1}{\sqrt{1-x^2}}\)
\(\frac{d}{dx}\tan^{-1}x=-\frac{1}{1+x^2}\)
Integrals
\(\int af(x)\,dx=a\int f(x)\,dx\)
\(\int[f(x)+g(x)]\,dx=\int f(x)\,dx+\int g(x)\,dx\)
\(\int x^m\,dx=\frac{x^{m+1}}{m+1}\ (m\neq1) ~~~~~~=\ln x\ (m=-1)\)
\(\int\sin{x}\,dx=-\cos x\)
\(\int\cos{x}\,dx=\sin x\)
\(\int\tan{x}\,dx=\ln|\sec x|\)
\(\int\sin^2{ax}\,dx=\frac{x}{2}-\frac{\sin{2ax}}{4a}\)
\(\int\cos^2{ax}\,dx=\frac{x}{2}+\frac{\sin{2ax}}{4a}\)
\(\int\sin{ax}\cos{ax}\,dx=-\frac{\cos2ax}{4a}\)
\(\int e^{ax}\,dx=\frac{1}{a}e^{ax}\)
\(\int xe^{ax}\,dx=\frac{e^{ax}}{a^2}(ax-1)\)
\(\int\ln{ax}\,dx=x\ln{ax}-x\)
\(\int\frac{dx}{a^2+x^2}=\frac{1}{a}\tan^{-1}\frac{x}{a}\)
\(\int\frac{dx}{a^2-x^2}-\frac{1}{2a}\ln\left|\frac{x+a}{x-a}\right|\)
\(\int\frac{dx}{\sqrt{a^2+x^2}}=\sinh^{-1}\frac{x}{a}\)
\(\int\frac{dx}{\sqrt{a^2-x^2}}=\sin^{-1}\frac{x}{a}\)
\(\int\sqrt{a^2+x^2}\,dx=\frac{x}{2}\sqrt{a^2+x^2}+\frac{a^2}{2}\sinh^{-1}\frac{x}{a}\)
\(\int\sqrt{a^2-x^2}\,dx=\frac{x}{2}\int{a^2-x^2}+\frac{a^2}{2}\sin^{-1}\frac{x}{a}\)
Binomial Theorem
\((1+x)^n=1 + \frac{nx}{1!}+\frac{n(n-1)x^2}{2!}+........(x^2 <1)\)
Exponential Expansion
\(e^x = 1 + x + \frac{x^2}{2!} +\frac{x^3}{3!}+.........\)
Logarithmic Expansion
\(ln(1+x) = x - \frac{1}{2}x^2 + \frac{1}{3}x^3 - .....(|x| <1)\)
Trigonometric Expansions \((\theta ~in ~radians)\)
\(\sin\theta = \theta -\frac{\theta^3}{3!}+\frac{\theta^5}{5!}-\frac{\theta^7}{7!}+......\)
\(\cos\theta = \theta -\frac{\theta^2}{2!}+\frac{\theta^4}{4!}-\frac{\theta^6}{6!}+......\)
\(\tan\theta = \theta + \frac{\theta^3}{3}+\frac{2\theta^5}{15}+\frac{17\theta^7}{315}+.....\)+\(\frac{2^{2n}(2^n-1)B_n\theta^{2n-1}}{(2n)!}+......\)
\(\sec\theta = 1 + \frac{\theta^2}{2}+\frac{5\theta^4}{24}+\frac{61\theta^6}{720}+.....\)\(+ \frac{E_n\theta^{2n}}{(2n)!}+......\)
where \(B_n\) and \(E_n\) are Bernoulli and Euler Numbers, respectively.
Scalar Products
The dot product or scalar product of two vectors \(\vec a\) and \(\vec b\):
\[\begin{equation} {\vec a} \cdot {\vec b} \equiv a_x b_x + a_y b_y + a_z b_z = {\rm scalar~number}. \end{equation}\]
Let us rotate the coordinate axes though \(\theta\) degrees about \(Oz\). Then, \({\vec a} \cdot {\vec b}\) takes the following form in the new coordinate system.
\(\vec a \cdot \vec b\) \(=(a_x\cos\theta+a_y\sin\theta)(b_x\cos\theta + b_y\sin\theta)\)
\((-a_x\sin\theta + a_y\cos\theta)(-b_x\sin \theta + b_y\cos\theta) +a_z b_z\)
\(=a_x b_x + a_y b_y + a_z b_z\)
Thus, \({\vec a} \cdot {\vec b}\) is invariant under rotation about \(Oz\). Similarly, it can easily be shown that it is also invariant under rotation about \(Ox\) and \(Oy\). Therefore, \({\vec a} \cdot {\vec b}\) is a scalar, and that the above definition is well established.
It cab be easily shown that the dot product follows the commutative and distributive laws of algebra:
\({\vec a} \cdot {\vec b}\) \({=\vec b} \cdot {\vec a},\)
\({\vec a}\cdot({\vec b}+{\vec c})\) \({=\vec a} \cdot {\vec b} + {\vec a}\cdot {\vec c}.\)
We have shown that the dot product \({\vec a} \cdot {\vec b}\) is coordinate independent. But what is the geometric significance of this? In the special case where \({\vec a} = {\vec b}\), we get
\[\begin{equation} {\vec a} \cdot {\vec b} = a_x^{~2}+a_y^{~2} + a_z^{~2} = \vert{\vec a}\vert^2=a^2. \end{equation}\]
So, the invariance of \({\vec a} \cdot {\vec a}\) is equivalent to the invariance of the magnitude of vector \({\bf a}\) under transformation.
Let us now investigate the general case. The length squared of \(AB\) in the vector triangle as shown in Figure A-4 is

\[\begin{equation} ({\vec b} - {\vec a} ) \cdot ({\vec b} - {\vec a} ) = \vert{\vec a}\vert^2 + \vert{\vec b}\vert^2 - 2\,{\vec a} \cdot {\vec b}. \end{equation}\]
Applying the “cosine rule” of trigonometry, we get
\[\begin{equation} (AB)^2 = (OA)^2 + (OB)^2 - 2 \,(OA)\,(OB)\,\cos\theta, \end{equation}\]
where \((AB)\) denotes the length of side \(AB\). It follows that
\[\begin{equation} {\vec a} \cdot {\vec b} = {|\vec a|} {|\vec b|}\cos\theta. \end{equation}\]
In this case, the invariance of \({\vec a} \cdot {\vec b}\) under transformation is equivalent to the invariance of the angle subtended between the two vectors. Note that if \({\vec a} \cdot {\vec b} =0\) then either \({|\vec a|}=0\), \({|\vec b|}=0\), or the vectors \(\vec a\) and \(\vec b\) are mutually perpendicular. The angle subtended between two vectors can easily be obtained from the dot product as follows:
\[\begin{equation} \cos\theta = \frac{{\vec a} \cdot {\vec b}}{{|\vec a|}{|\vec b|}}. \end{equation}\]
The work \(W\) performed by a constant force \(\vec F\) which moves an object through a displacement \(\vec r\) is the product of the magnitude of \(\vec F\) times the displacement in the direction of \(\vec F\). If the angle subtended between \(\vec F\) and \(\vec r\) is \(\theta\) then
\[\begin{equation} W = {|\vec F|}({|\vec r|}\cos\theta) = {\vec F}\cdot {\vec r}. \end{equation}\]
The work \(dW\) performed by a non-constant force \({\vec F}\) which moves an object through an infinitesimal displacement \(d{\vec r}\) in a time interval \(dt\) is \(dW={\vec F}\cdot d{\vec r}\). Thus, the rate at which the force does work on the object, which is usually referred to as the power, is \(P = dW/dt = {\vec F}\cdot d{\vec r}/dt\), or \(P={\vec F}\cdot {\vec v}\), where \({\vec v} = d{\vec r}/dt\) is the object’s instantaneous velocity.
Vector Product
Let’s, consider, the cross product or vector product:
\[\begin{equation} {\vec a}\times{\vec b} \equiv (a_y \, b_z-a_z\, b_y,\, a_z\, b_x - a_x\, b_z,\, a_x\, b_y - a_y\, b_x) ={\vec c}. \end{equation}\]
Let’s rotate the coordinate axes through an angle \(\theta\) about \(Oz\). In the new coordinate system,
\(c_{x'}\) \(=\) \((-a_x\, \sin\theta + a_y\,\cos\theta)\,b_z - a_z\,(-b_x\, \sin\theta + b_y\,\cos\theta)\)
\(=\) \((a_y\, b_z - a_z\, b_y)\, \cos\theta + (a_z\, b_x-a_x\, b_z)\,\sin\theta\)
\(=\) \(c_x\,\cos\theta +c_y\,\sin\theta.\)
Thus, the \(x\)-component of \({\vec a}\times{\vec b}\) transforms correctly. It can easily be shown that the other components transform correctly as well, and that all components also transform correctly under rotation about \(Ox\) and \(Oy\). Thus, \({\vec a}\times{\vec b}\) is a proper vector. Incidentally, \({\vec a}\times{\vec b}\) is the only simple combination of the components of two vectors that transforms like a vector (which is non-coplanar with \({\vec a}\) and \({\vec b}\)). Unlike the dot or scalar product of vectors, the cross product does not hold commutative law,
\[\begin{equation} {\vec a}\times{\vec b} = - {\vec b} \times{\vec a}, \end{equation}\]
however it holds distributive law,
\[\begin{equation} {\vec a}\times({\vec b} +{\vec c})= {\vec a} \times{\vec b}+{\vec a}\times{\vec c}, \end{equation}\]
but it does not hold associative law,
\[\begin{equation} {\vec a}\times({\vec b} \times{\vec c})\neq ({\vec a}\times{\vec b}) \times{\vec c}. \end{equation}\]
The cross product transforms like a vector, which means that it must have a well-defined direction and magnitude. We can show that \({\vec a}\times{\vec b}\) is perpendicular to both \({\vec a}\) and \({\vec b}\). Consider \({\vec a}\cdot {\vec a}\times{\vec b}\). If this is zero then the cross product must be perpendicular to \({\vec a}\). Now,
\({\vec a}\cdot {\vec a}\times{\vec b}\) \(=\) \(a_x\,(a_y\, b_z-a_z\, b_y) + a_y\, (a_z\, b_x- a_x \,b_z) +a_z\,(a_x \,b_y - a_y\, b_x)\)
\(=\) \(0.\)
Therefore, \({\vec a}\times{\vec b}\) is perpendicular to \({\vec a}\). Likewise, it can be demonstrated that \({\bf a}\times{\vec b}\) is perpendicular to \({\vec b}\). The vectors \(\vec a\), \(\vec b\), and \({\vec a}\times{\vec b}\) form a right-handed set, like the unit vectors \({\vec e}_x\), \({\vec e}_y\), and \({\vec e}_z\). In fact, \({\vec e}_x\times {\vec e}_y={\vec e}_z\). This defines a unique direction for \({\vec a}\times{\vec b}\), which is obtained from a right-hand rule as shown in Figure A-5 below:
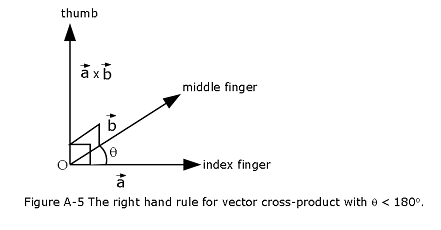
Let us now calculate the magnitude of \({\vec a}\times{\vec b}\). We have
\(({\vec a}\times{\vec b})^2\) = \((a_y \,b_z-a_z\, b_y)^2 +(a_z \,b_x - a_x\, b_z)^2 +(a_x \,b_y-a_y \,b_x)^2\)
\(=(a_x^{~2}+a_y^{~2}+a_z^{~2})\,(b_x^{~2}+b_y^{~2}+b_z^{~2})-(a_x\, b_x + a_y \,b_y + a_z\, b_z)^2\)
\(=\displaystyle \vert{\vec a}\vert^2 \,\vert{\vec b}\vert^2 - ({\vec a}\cdot {\vec b})^2\)
\(={|\vec a|^2}{|\vec b|^2}-({|\vec a|}\cdot{|\vec b|})^2 = {|\vec a|^2}{|\vec b|^2}-{|\vec a|^2}{|\vec b|^2}\cos^2\theta\) \(= {|\vec a|^2}{|\vec b|^2}\sin^2\theta\)
Thus,
\[\begin{equation} \vert{\vec a}\times{\vec b}\vert = \vert{\vec a}\vert\,\vert{\vec b}\vert\,\sin\theta, \end{equation}\]
where \(\theta\) is the angle subtended between \({\vec a}\) and \({\vec b}\). Clearly, \({\vec a}\times{\vec a} = {\vec0}\) for any vector, since \(\theta\) is always zero in this case. Also, if \({\vec a}\times{\vec b} = {\vec0}\) then either \(\vert{\vec a}\vert=0\), \(\vert{\vec b}\vert=0\), or \({\bf b}\) is parallel (or antiparallel) to \({\bf a}\).
Consider the parallelogram defined by the vectors \({\vec a}\) and \({\vec b}\) as shown in Figure A-6 below. The scalar area of the parallelogram is \(a\,b \sin\theta\). By convention, the vector area has the magnitude of the scalar area, and is normal to the plane of the parallelogram, in the sense obtained from a right-hand circulation rule by rotating \({\vec a}\) on to \({\vec b}\) (through an acute angle): i.e., if the fingers of the right-hand circulate in the direction of rotation then the thumb of the right-hand indicates the direction of the vector area. So, the vector area is coming out of the page in Figure A-6.
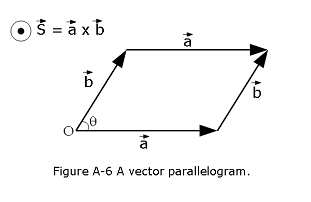
It follows that
\[\begin{equation} {\vec S} = {\vec a}\times {\vec b}, \end{equation}\]
Suppose that a force \({\vec F}\) is applied at position \({\vec r}\) Figure A-7. The torque about the origin \(O\) is the product of the magnitude of the force and the length of the lever arm \(OQ\). Thus, the magnitude of the torque is \(\vert{\vec F}\vert\,\vert{\vec r}\vert\,\sin\theta\). The direction of the torque is conventionally defined as the direction of the axis through \(O\) about which the force tries to rotate objects, in the sense determined by a right-hand circulation rule. Hence, the torque is out of the page in Figure A-7.
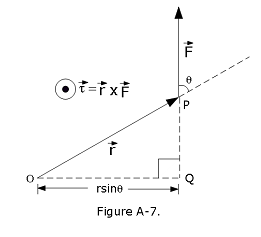
It follows that the vector torque is given by
\[\begin{equation} \vec\tau= {\vec r}\times{\vec F}. \end{equation}\]
The angular momentum, \({\vec l}\), of a particle of linear momentum \({\vec p}\) and position vector \({\vec r}\) is simply defined as the moment of its momentum about the origin: i.e.,
\[\begin{equation} {\vec l}={\vec r}\times {\vec p}. \end{equation}\]
Products of Vectors: Unit Vector Notation
\(\vec a \times \vec b = -\vec b \times \vec a = \begin{vmatrix} \hat i & \hat j & \hat k \\ a_x & a_y & a_z \\ b_x & b_y & b_z \end{vmatrix}\)
\(=\hat i\begin{vmatrix} a_y & a_z \\ b_y & b_z \end{vmatrix} -\hat j\begin{vmatrix} a_x & a_z \\ b_x & b_z \end{vmatrix}+\hat k\begin{vmatrix} a_x & a_y \\ b_x & b_y \end{vmatrix}\)
\(=\left(a_y b_z-b_y a_z\right)\hat i+\left(a_z b_x-b_z a_x\right)\hat j\) \(+\left(a_x b_y-b_x a_y\right)\hat k\)
\(\left|\vec a \times \vec b\right|=ab\sin\theta\)
\(\vec a.(\vec b \times \vec c)=\vec b.(\vec c \times \vec a)=\vec c.(\vec a \times \vec b)\) \(\vec a \times (\vec b \times \vec c) = (\vec a.\vec c)\vec b - (\vec a.\vec b)\vec c\)
Cramer’s Rule
Two simultaneous equations in unknowns x and y, \(a_1x+b_1y=c_1~~~and~~~a_2x+b_2y=c_2\)
have the solutions
\(x=\frac{\begin{vmatrix} c_1 & b_1 \\ c_2 & b_2 \end{vmatrix}}{{\begin{vmatrix} a_1 & b_1 \\ a_2 & b_2 \end{vmatrix}}}=\frac{c_1b_2-c_2b_2}{a_1b_2-a_2b_1}\)
and
\(y=\frac{\begin{vmatrix} a_1 & c_1 \\ a_2 & c_2 \end{vmatrix}}{{\begin{vmatrix} a_1 & b_1 \\ a_2 & b_2 \end{vmatrix}}}=\frac{a_1c_2-a_2c_1}{a_1b_2-a_2b_1}\)