Chapter 6 Current and Resistance

Learning Objectives:

In this chapter you will basically learn:

\(\bullet\) Learn the electric current as the rate at which charge moves through a point, in a given time interval.

\(\bullet\) Learn that current is due to the motion of conduction electrons that are driven by electric fields set up in a wire by a battery.

\(\bullet\) Learn the definition of current density and a current density vector.

\(\bullet\) Learn the relationship between the current through a cross section of a conductor with the current density vector and the element area vector over the full cross section.

\(\bullet\) Learn the motion of conduction electrons in terms of their drift speed, current density J, charge carrier density n.

\(\bullet\) Learn how the electric field magnitude E set up at a point in a given material with resistivity \(\rho\), and the resulting current density magnitude J at that point.

\(\bullet\) Learn how a uniform electric field ca be set up in a wire, and how the electric field magnitude E, the potential difference V between the two ends, and the wire’s length L are related.

\(\bullet\) Learn how electric resistance R of an object, its resistivity \(\rho\), its length L, and its crosssectional area A are related.

\(\bullet\) Learn the relationship that holds between the conductor’s resistivity \(\rho\) as a function of temperature T.

\(\bullet\) Learn the materials that obeys Ohm’s law and one that does not.

\(\bullet\) Learn the relationship between resistivity \(\rho\), number density n of conduction electrons, and the mean free time \(\tau\) of the electrons.

\(\bullet\) Learn how a in a resistive device, electric power P, current i, voltage V, and resistance R are related.

\(\bullet\) Learn how to distinguish conductors, semiconductors, and superconductors.

6.1 Electric Current:

In this chapter we will study how static charges once gets accelerated by the applicaton of electrical field using a voltage source called battery. As the charges start moving the potential energy changes to kinetic energy as they traveled through a potential difference where the electrical field did work on the charge.

The average electrical current i is the rate at which dq charge flows through a cross section of a conductor, in which current i has been established. If charge dq passes through a conductor in time dt, then the current i through that conductor is defined as

\[\begin{equation} i =\frac{dq}{dt} \tag{6.1} \end{equation}\]

We can find the charge that passes through the plane in a time interval from 0 to t by integration:

\[\begin{equation} q = \int dq = \int_{0}^{t}i dt \tag{6.2} \end{equation}\]

The SI unit for current is the coulomb per second, or the ampere (A), is defined as follows:

\[1~ampere = 1~A = 1~coulomb~per~second = 1~C/s\] EXAMPLE 6-1

The purpose of having a battery in an automobile is to run the electric starter motor, which starts the engine. The operation of starting the vehicle requires a large current to be supplied by the battery. Once the engine starts, a device called an alternator takes over supplying the electric power required for running the vehicle and for charging the battery.

1. What is the average current involved when an automotive battery sets in motion \(720~\mathrm{C}\) of charge in \(4.00~\mathrm{s}\) while starting an engine? (b) How long does it take \(1.00~\mathrm{C}\) of charge to flow from the battery?

Solution: a. Using Eqn.6-1

\[i=\frac{dq}{dt}=\frac{720~\mathrm{C}}{4.00~\mathrm{s}}=180~\mathrm{C/s}=180~\mathrm{A}.\]

2. Time it takes to flow \(1.00~\mathrm{C}\) of charge from the battery?

\[ dt=\frac{dq}{i}=\frac{1.00~\mathrm{C}}{180~\mathrm{C/s}}=5.56\times10^{-3}~\mathrm{s}=5.56~\mathrm{ms}.\]

6.2 Current Density:

Current density \(\vec J\) a new quantity which has the same direction as the velocity of the moving charges if they are positive and the opposite direction if they are negative. For each element of the cross section, the magnitude J is equal to the current per unit area through that element. We can write the amount of current through the element as \(\vec J.d\vec A\) where \(d\vec A\) is the area vector of the element, perpendicular to the element.The total current through the surface is then

\[\begin{equation} i = \int \vec J.d\vec A \tag{6.3} \end{equation}\]

If the current is uniform across the surface and parallel to \(d\vec A\)then \(\vec J\)is also uniform and parallel \(d\vec A\) to then Eq. 6-3 becomes

\[i = \int J~dA=J\int~dA=JA\] Therefore,

\[\begin{equation} J = \frac {i}{A} \tag{6.4} \end{equation}\]

6.3 Resistance and Resistivity:

When a voltage is applied to a conductor, an electrical field \(\vec{\mathbf{E}}\) is created, and charges are forced to flow due to the electrical field. The current density \(\vec{\mathbf{J}}\) that results depends on the electrical field and the properties of the material. This dependence can be very complex. In some materials, including metals at a given temperature, the current density is approximately proportional to the electrical field. In these cases, the current density can be modeled as

\[\vec{\mathbf{J}}=\sigma\vec{\mathbf{E}}\]

where \(\sigma\) is the electrical conductivity. The electrical conductivity is analogous to thermal conductivity and is a measure of a material’s ability to conduct or transmit electricity. Conductors have a higher electrical conductivity than insulators. Since the electrical conductivity is \(\sigma=J/E\), the units are

\[\sigma=\frac{[J]}{[E]}=\frac{\mathrm{A/m}^2}{\mathrm{V/m}}=\frac{\mathrm{A}}{\mathrm{V}\cdot\mathrm{m}}\]

Here, we define a unit named the ohm with the Greek symbol uppercase omega, \(\Omega\). The unit is named after Georg Simon Ohm. One ohm equals one volt per amp: \(1~\Omega=1~\mathrm{V/A}\). The units of electrical conductivity are therefore \((\Omega\cdot\mathrm{m})^{-1}\).

Conductivity is an intrinsic property of a material. Another intrinsic property of a material is the resistivity, or electrical resistivity. The resistivity of a material is a measure of how strongly a material opposes the flow of electrical current. The symbol for resistivity is the lowercase Greek letter rho, \(\rho\), and resistivity is the reciprocal of electrical conductivity:

\[\rho=\frac{1}{\sigma}\]

The unit of resistivity in SI units is the ohm-meter \((\Omega\cdot\mathrm{m})\). We can define the resistivity in terms of the electrical field and the current density,

\[\begin{equation} \rho=\frac{E}{J} \tag{6.5} \end{equation}\]

The resistance R of a conducting wire of length L and uniform cross section is where A is the cross-sectional area is directly proportional to resistivity \(\rho\).

\[\begin{equation} R= \frac{\rho L}{A} \tag{6.6} \end{equation}\]

The greater the resistivity, the larger the field needed to produce a given current density. The lower the resistivity, the larger the current density produced by a given electrical field. Good conductors have a high conductivity and low resistivity. Good insulators have a low conductivity and a high resistivity. Table 5.3.1 lists resistivity and conductivity values for various materials.

EXAMPLE 6-2 Calculate the current density, resistance, and electrical field of a \(5{\text -}\mathrm{m}\) length of copper wire with a diameter of \(2.053~\mathrm{mm}\) \((12{\text -}\mathrm{gauge})\) carrying a current of \(i=10~\mathrm{mA}\).

Solution: First, we calculate the current density:

\[J=\frac{i}{A}=\frac{10\times10^{-3}~\mathrm{A}}{3.31\times10^{-6}~\mathrm{m}^2}=3.02\times10^3~\mathrm{A/m}^2\]

The resistance of the wire is

\[R= \frac{\rho L}{A}=\frac{(1.68\times10^{-8}~\Omega\cdot\mathrm{m})(5.00~\mathrm{m})}{3.31\times10^{-6}~\mathrm{m}^2}=0.025~\Omega\]

Finally, we can find the electrical field:

\[E=\rho J=(1.68\times10^{-8}~\Omega\cdot\mathrm{m})\left(3.02\times10^3~\mathrm{A/m}^2\right)=5.07\times10^{-5}~\mathrm{V/m}\]

Table 6-1 List of resistivities of some useful materials at room temperature (\(20^\circ~C\)).

Material	Resistivity, \(\rho\)(\(\Omega.m)\)	Temperature coefficient of resistivity, \(\alpha ~ (K^{-1})\)
	\(\mathbb{Typical~Metals}\)
Silver	\(1.62\times 10^{-8}\)	\(4.1\times 10^{-3}\)
Copper	\(1.69\times 10^{-8}\)	\(4.3\times 10^{-3}\)
Gold	\(2.35\times 10^{-8}\)	\(4.0\times 10^{-3}\)
Aluminum	\(2.75\times 10^{-8}\)	\(4.4\times 10^{-3}\)
\(Manganin^a\)	\(4.82\times 10^{-8}\)	\(0.002\times 10^{-3}\)
Tungsten	\(5.25\times 10^{-8}\)	\(4.5\times 10^{-3}\)
Iron	\(9.68\times 10^{-8}\)	\(6.5\times 10^{-3}\)
Platinum	\(10.6\times 10^{-8}\)	\(3.9\times 10^{-3}\)
	\(\mathbb{Typical~Semiconductors}\)
Silicon, pure	\(2.5\times 10^{3}\)	\(-70\times 10^{-3}\)
\(Silicon^b\), n-type	\(8.7\times 10^{-4}\)
\(Silicon^c\), p-type	\(2.8\times 10^{-3}\)
	\(\mathbb{Typical~Insulators}\)
Glass	\(10^{10}-10^{14}\)
Fused quartz	\(\sim 10^{16}\)

Looking at Table 6.1, we can see a column labeled “Temperature Coefficient of Resistivity \(\alpha\).” In most of the conducting metals, the resistivity increases with increasing temperature. The increasing temperature causes increased vibrations of the atoms in the lattice structure of the metals, which impede the motion of the electrons. In many materials, the dependence is approximately linear and can be modeled using a linear equation:

\[\begin{equation} \rho\approx\rho_0[1+\alpha(T-T_0)], \tag{6.7} \end{equation}\]

where \(\rho\) is the resistivity of the material at temperature T, \(\alpha\) is the temperature coefficient of the material, and \(\rho_0\) is the resistivity at \(T_0\), usually taken as reference temperature.

One can notice that the temperature coefficient \(\alpha\) is negative for the semiconductors listed in Table 6.1, meaning that their resistivity decreases with increasing temperature. As a result semiconductors become better conductor at higher temperature, because increased thermal agitation increases the number of free charges available to carry current. This property of decreasing \(\rho\) with temperature is also related to the type and amount of impurities present in the semiconductors.

6.4 Ohm’s Law:

If we apply the same potential difference between the ends of geometrically similar rods of copper and of glass, very different currents result. The characteristic of the conductor that enters here is its electrical resistance. We determine the resistance between any two points of a conductor by applying a potential difference V between those points and measuring the current i that results.The resistance R is then

\[\begin{equation} R = \frac{V}{i}~~~(Definition~of~R) \tag{6.8} \end{equation}\]

The SI unit for resistance that follows from Eq. 6-7 is the volt per ampere is named as ohm (\(\Omega\)) as given below:

\[\begin{equation} 1~ohm = 1~\Omega = 1~\frac{V}{A} \tag{6.9} \end{equation}\]

The resistor can be used to reduce current flow or provide a voltage drop. shows the symbols used for a resistor in schematic diagrams of a circuit. Two commonly used standards for circuit diagrams as shown in Figure 6.1 are provided by the American National Standard Institute (ANSI) and the International Electrotechnical Commission (IEC).

The most common material used to make a resistor is carbon. A carbon track is wrapped around a ceramic core, and two copper leads are attached. A second type of resistor is the metal film resistor, which also has a ceramic core. The track is made from a metal oxide material, which has semiconductive properties similar to carbon. Again, copper leads are inserted into the ends of the resistor. The resistor is then painted and marked for identification. A resistor has four colored bands, as shown in Figure 6.2.

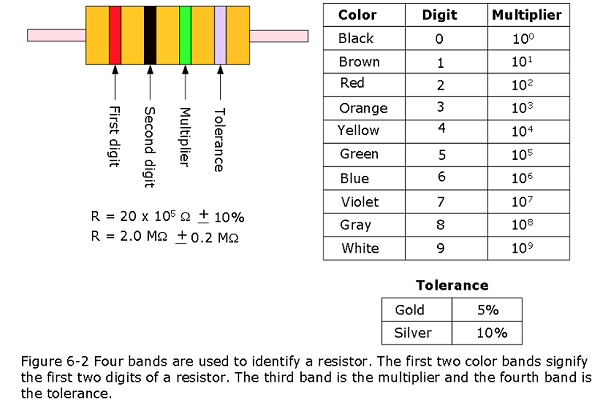
Figure 6-3 (a) A potential difference V is applied to the terminals of a device, establishing a current i. (b) A plot of current i versus applied potential difference V when the device is a 1000 0 resistor. (c) A plot when the device is a semiconducting pn junction diode.

EXAMPLE 6.5.1

A tungsten filament at \(20~^{\circ}\mathrm{C}\) has a resistance of \(0.350~\Omega\). What would the resistance be if the temperature is increased to \(2850~^{\circ}\mathrm{C}\)?

Solution The resistance of the hotter filament R is obtained by entering known values into the above equation:

\[R=R_0(1+\alpha\Delta T)=(0.350~\Omega)\left[1+\left(4.5\times10^{-3}~(^{\circ}\mathrm{C})^{-1}\right)(2850~^{\circ}\mathrm{C})\right]=4.8~\Omega\] EXAMPLE 6.5.2

Long cables can sometimes act like antennas, picking up electronic noise, which are signals from other equipment and appliances. Coaxial cables are used for many applications that require this noise to be eliminated. Coaxial cables consist of an inner conductor of radius \(r_i\) surrounded by a second, outer concentric conductor with radius \(r_0\) (Figure 6.4). The space between the two is normally filled with an insulator such as polyethylene plastic. A small amount of radial leakage current occurs between the two conductors. Determine the resistance of a coaxial cable of length L.

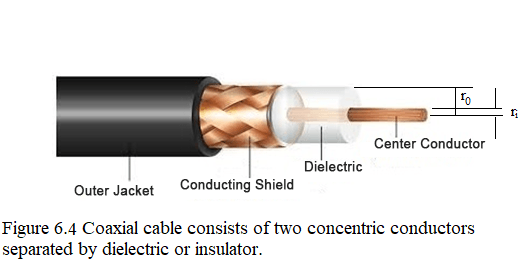
Considering the differential resistance \(dR\) of a coaxial cable of length L with area \(A = 2\pi rL\) and integrating we find the resistance of a coaxial cable of length L:

\[dR = \frac {\rho dr}{2\pi rL}\]

\[\begin{eqnarray} R =\int_{r_i}^{r_0}\frac{\rho}{2\pi rL}dr=\frac{\rho}{2\pi L}\int_{r_i}^{r_0}\frac{1}{r}dr=\frac{\rho}{2\pi L}\ln\frac{r_0}{r_i} \end{eqnarray}\]

6.5 A Microscopic View of Ohm’s Law:

6.6 Electric Power:

Figure 6-5 shows a circuit consisting of a battery B that is connected by wires, with negligible resistance and is connected to a device might be a resistor, a storage battery (a rechargeable battery), a motor, or some other electrical device.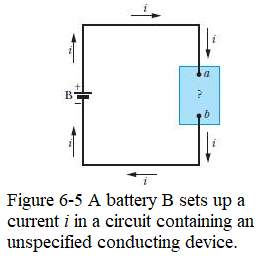

The battery maintains a potential difference of magnitude V across its own terminals and thus (because of the wires) across the terminals of the unspecified device, with a greater potential at terminal a of the device than at terminal b. Because there is an external conducting path between the two terminals of the battery, and because the potential differences set up by the battery are maintained, a steady current i is produced in the circuit, directed from terminal a to terminal b. The amount of charge dq that moves between those terminals in time interval dt is equal to i dt.This charge dq moves through a decrease in potential of magnitude V, and thus its electric potential energy decreases in magnitude by the amount dU

\[\begin{equation} dU = dq~V = idt~V \tag{6.10} \end{equation}\]

The power P associated with that transfer is the rate of transfer dU/dt, which is given by Eq. 26-25 as

\[\begin{equation} P= \frac{dU}{dt} = iV \tag{6.11} \end{equation}\]

The SI unit of power that follows from Eq. 6-11 is the volt-ampere (V.A). We can write it as

\[1~V.A=(1\frac{J}{C})(1\frac{C}{s})=1\frac{J}{s}=1~W\] For a resistor or some other device with resistance R, we can combine Eqs. 6-8 (\(R = \frac{V}{i}\)) and (6-11) (\(P = i~V\)) to obtain, for the rate of electrical energy dissipation due to a resistance, either

\[\begin{equation} P = i^2~R ~~~(resistive~dissipation) \tag{6.12} \end{equation}\]

or

\[\begin{equation} P = \frac{V^2}{R} ~~~(resistive~dissipation) \tag{6.13} \end{equation}\]

Caution: We must be careful to distinguish these two equations from Eq. 6-11: P = iV applies to electrical energy transfers of all kinds; \(P = i^2~R\) and \(P = \frac{V^2}{R}\) apply only to the transfer of electric potential energy to thermal energy in a device with resistance.

EXAMPLE 6.7.1 A DC winch motor is rated at \(20.0~\mathrm{A}\) with a voltage of \(115~\mathrm{V}\). When the motor is running at its maximum power, it can lift an object with a weight of \(4.90\times10^3~\mathrm{N}\) a distance of \(10.0~\mathrm{m}\), in \(30.0~\mathrm{s}\), at a constant speed. (a) What is the power consumed by the motor? (b) What is the power used in lifting the object? Ignore air resistance. (c) Assuming that the difference in the power consumed by the motor and the power used lifting the object are dissipated as heat by the resistance of the motor, estimate the resistance of the motor?

Solution: a. The power consumed by the motor is equal to P=iV and the current is given as \(20.0~\mathrm{A}\) and the voltage is \(115~\mathrm{V}\):

\[P=IV=(20.0~\mathrm{A})(115~\mathrm{V})=2.30\times10^{3}~\mathrm{W}\]

2. The power used lifting the object is equal to P=Fv where the force is equal to the weight of the object \((1960~\mathrm{N})\) and the magnitude of the velocity is \(v=\frac{10.0~\mathrm{m}}{30.0~\mathrm{s}}=0.333~\mathrm{m/s}\),

\[P=Fv=(4.90\times10^3~\mathrm{N})(0.333~\mathrm{m/s})=1.63\times10^{3}~\mathrm{W}\]

3. The difference in the power equals \(2.30\times10^{3}~\mathrm{W}-1.63\times10^{3}~\mathrm{W}=0.67\times10^3~\mathrm{W}\)$ and the resistance can be found using \(P=i^2R\):

\[R=\frac{P}{I^2}=\frac{0.67\times10^{3}~\mathrm{W}}{(20.0~\mathrm{A})^2}=1.7~\Omega\] EXAMPLE 6.7.2 The simple way to save electric power is to replace a \(100{\text -}\mathrm{W}\) incandescent bulb with a \(20{\text -}\mathrm{W}\) LED bulb. The \(20{\text -}\mathrm{W}\) LED bulb can provide the same amount of light output as the \(100{\text -}\mathrm{W}\) incandescent light bulb. What is the cost savings for using the LED bulb in place of the incandescent bulb for one year, assuming \(\$ 0.10\) per kilowatt-hour is the average energy rate charged by the power company? Assume that the bulb is turned on for three hours a day.

Solution a. Calculate the power for each bulb.

\[E_{Incandescent} = Pt=100~W\left(\frac{1~kW}{1000~W}\right)\left(\frac{3~h}{day}\right)(365~days)=109.5~kW \cdot h\] \[E_{LED}=Pt=20~W\left(\frac{1~kW}{1000~W}\right)\left(\frac{3~h}{day}\right)(365~days)=21.9~kW\cdot h\]

2. Calculate the cost for each.

\[Cost_{Incandescent} = 109.5~kW\cdot h\left(\frac{$0.10}{kW \cdot h}\right)= $10.95\] \[Cost_{LED} = 21.9~kW\cdot h\left(\frac{$0.10}{kW \cdot h}\right) = $2.19\]

6.7 Semiconductors, Superconductors:

A semiconductor material has an electrical conductivity which is in between that of a conductor, such as metallic copper, and an insulator, such as glass. Pure semiconducting materials such as Si is an insulator. The intrinsic Si property may be altered by adding impurities (“dopants”) into the crystal structure. The conductivity of silicon is increased by adding either a pentavalent (antimony, phosphorus, or arsenic) or trivalent (boron, gallium, indium) atoms to change to extrinsic semiconductors. A doped semiconductor mostly containing free electrons is known as “n-type” when it contains mostly free holes it is called “p-type”.

Two kinds of dopants can be added in the same crystal, to create a semiconductor junction is called p-n junction diode. A p-n junction diode is the fundamental building block of modern semiconducting devices from which the development of the transistor in 1947, the integrated circuit in 1958, and the MOSFET (metal–oxide–semiconductor field-effect transistor) in 1959 happened. The second most useful semiconductor is known as gallium arsenide (GaAs) and is used for laser diodes, and various other high frequency and fast devices. Silicon is a high temperature resistant semiconductor widely used for fabricating most of the microelectronic circuits, chips, microprocessors, LED etc. However, Si cannot be used to fabricate diode laser because of its inherent limitation having indirect bandgap semiconductor.

Table 6-2 compares the properties of silicon— a typical semiconductor—and copper—a typical metallic conductor. We see that silicon has many fewer charge carriers, a much higher resistivity, and a temperature coefficient of resistivity that is both large and negative.Thus, although the resistivity of copper increases with increasing temperature, that of pure silicon decreases.

Table 6-2 Some Electrical Properties of Copper and Silicon.

Property	Copper	Silicon
Type of Material	Metal	Semiconductor
Charge carrier density, \(m^{-3}\)	\(8.49\times 10^{28}\)	\(1.0\times 10^{16}\)
Resistivity,\(\Omega.m\)	\(1.69\times 10^{-8}\)	\(2.5\times 10^{3}\)
Temperature coefficient of resistivity,\(K^{-1}\)	\(+4.3\times 10^{-3}\)	\(-70\times 10^{-3}\)

Superconductors in which charge can flow through a superconducting conductor without losing its energy to thermal energy was first demonstrated inn 1911, by a Dutch physicist Kamerlingh Onnes. He observed that the resistivity of mercury absolutely disappears at temperatures below about 4 K (Fig. 6-6). In 1986, however, new ceramic materials were discovered that become superconducting at considerably higher (and thus cheaper to produce) temperatures. Practical application of superconducting devices at room temperature may eventually become commonplace.

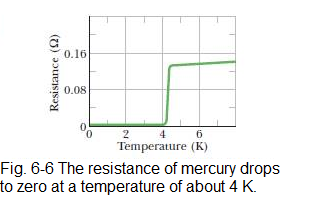
Superconductivity is a phenomenon much different from conductivity. In fact, the best of the normal conductors, such as silver and copper, cannot become superconducting at any temperature, and the new ceramic superconductors are actually good insulators when they are not at low enough temperatures to be in a superconducting state.

The complete microscopic theory of superconductivity was finally proposed in 1957 by Bardeen, Cooper and Schrieffer [1].This BCS theory explained the superconducting current as a superfluid of Cooper pairs, pairs of electrons interacting through the exchange of phonons. For this work, the authors were awarded the Nobel Prize in 1972. A theory of superconductivity is presented, based on the fact that the interaction between electrons resulting from virtual exchange of phonons is attractive when the energy difference between the electrons states involved is less than the phonon energy, \(\hbar \omega\).

[1] J. Bardeen; L. N. Cooper & J. R. Schrieffer (1957). “Theory of Superconductivity”. Physical Review. 108 (5): 1175–1205. Bibcode:1957PhRv..108.1175B. doi:10.1103/PhysRev.108.1175

Solved Problems Current & Resistance

1. [1] During the 4.0 min a 5.0 A current is set up in a wire, how many (a) coulombs and (b) electrons pass through any cross section across the wire’s width?

Solution:

1. Number of couloms pass through the cross section is \[q = it =(5.0~A)(4~min)(60~s/1~min)=1.2\times 10^3~C~(Answer).\]
2. Number of electrons pass through during the 4 minutes is \[n = \frac{q}{e}=\frac{1.2\times 10^3~C}{1.6\times 10^{-19}}~C = 7.5\times 10^{21}.~(Answer)\]

2. [3] A charged belt, 50 cm wide, travels at 30 m/s between a source of charge and a sphere. The belt carries charge into the sphere at a rate corresponding to \(100 \times 10^{-6}~A\). Compute the surface charge density on the belt.

Solution:

We know \(i = \frac{q}{t}\), \(v = \frac{s}{t}\), \(s = vt\), therefore, the charge density on the belt, \[\sigma = \frac{q}{A} = \frac{it}{ws}=\frac{it}{wvt}=\frac{i}{wv}=\frac{100 \times 10^{-6}~A}{(50\times 10^{-2}~m)(30~m/s)} = 6.67\times 10^{-6}~C/m^2~(Answer)\]

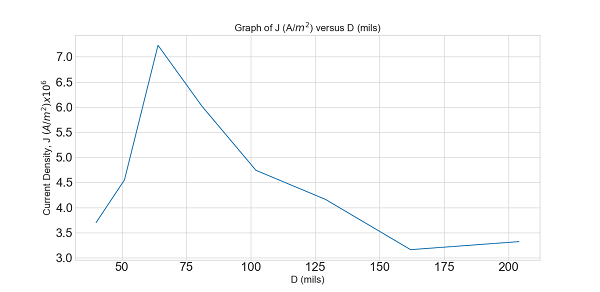
3. [4] The (United States) National Electric Code, which sets maximum safe currents for insulated copper wires of various diameters, is given (in part) in the table. Plot the safe current density as a function of diameter. Which wire gauge has the maximum safe current density? (“Gauge” is a way of identifying wire diameters, and 1 mil = \(10^{-3}~ in.\)

Gauge	4	6	8	10	12	14	16	18
Diameter in mils	204	162	129	102	81	64	51	40
Diameter \(\times 10^{-3}\) m	\(5.1816\)	\(4.1148\)	\(3.2766\)	\(2.5908\)	\(2.0574\)	\(1.6256\)	\(1.2954\)	\(1.0160\)
Safe Current in A	70	50	35	25	20	15	6	3
Current density (\(J=\frac{4i}{\pi D^2}\)) \(\times 10^6\) \(A/m^2\)	3.32	3.16	4.16	4.74	6.02	7.23	4.55	3.70

4. [8] A small but measurable current of \(1.2 \times 10^{-10}\) A exists in a copper wire whose diameter is 2.5 mm. The number of charge carriers per unit volume is \(8.49 \times 10^{28} m^3\). Assuming the current is uniform, calculate the (a) current density and (b) electron drift speed.

Solution:

1. Current density, \[J = i/A = \frac{4i}{\pi D^2}=\frac{4\times 1.2 \times 10^{-10}~A}{\pi (2.5\times 10^{-3}~m)^2}=2.44\times 10^{-5}~A/m^2~(Answer)\]
2. Electron drift speed, \[v_d = \frac{J}{ne}=\frac{2.44\times 10^{-5}~A/m^2}{(8.49 \times 10^{28} ~m^3)(1.6\times 10^{-19}~C)}=1.796\times 10^{-15}~m/s~(Answer)\]

5. [10] The magnitude J of the current density in a certain lab wire with a circular cross section of radius R = 2.00 mm is given by J = \((3.00 \times 10^8)r^2\), with J in amperes per square meter and radial distance r in meters. What is the current through the outer section bounded by r = 0.900R and r = R?

Solution:

The magnitude of current density \(J = \frac{di}{dA}\) and current can be calculated by integrating in the bounded cross section of r = 0.900R to r = R as follows: \[i = \int di=\int JdA = \int_{0.900R}^R(3\times 10^8)r^2(2\pi r)dr=(2\pi)(3\times 10^8)\left[\frac{r^4}{4}-\frac{(0.900r)^4}{4}\right]\]

\[i = (2\pi)(3\times 10^8)\left[\frac{r^4}{4}-\frac{(0.900r)^4}{4}\right]_{0.900R}^R\] \[i=(2\pi)(3\times 10^8)\left[\frac{16\times 10^{-12}}{4}-\frac{(0.6561)(16\times 10^{-12})}{4}\right]=25.93\times 10^{-4}~A/m^2~(Answer)\] 6. [11] What is the current in a wire of radius R = 3.40 mm if the magnitude of the current density is given by (a) \(J_a = J_0r/R\) and (b) \(J_b = J_0(1 - r/R)\), in which r is the radial distance and \(J_0 = 5.50 \times 10^4 ~A/m^2\)? (c) Which function maximizes the current density near the wire’s surface?

Solution: (a) Current with \(J_a = J_0r/R\) and \(J_0 = 5.50 \times 10^4 ~A/m^2\) is

\[i = \int di=\int J_adA =\int_0^R J_0(r/R)(2\pi r)dr=\int_0^R5.50 \times 10^4(r/R)(2\pi r)dr\] \[i = \int_0^R5.50 \times 10^4(r/R)(2\pi r)dr=2\pi(5.50\times 10^4)\left[\frac{r^3}{3R}\right]_0^R\] \[i =2\pi(5.50\times 10^4)\left[\frac{(3.4\times 10^{-3})^2}{3}\right]=1.33~A~(Answer)\] (b) Current with \(J_b = J_0(1 - r/R)\) and \(J_0 = 5.50 \times 10^4 ~A/m^2\) is

\[i = \int di=\int J_bdA =\int_0^RJ_0(1-(r/R)(2\pi r)dr=\int_0^R(5.50 \times 10^4)(1-(r/R)(2\pi r)dr\] \[i =\int_0^R(5.50 \times 10^4)(1-r/R)(2\pi r)dr=\frac{\pi R^2(5.50\times 10^4)}{3}=\frac{\pi (3.4\times 10^{-3})^2(5.50\times 10^4)}{3}=0.6658\approx = 0.666~A/m^2~(Answer)\] \[i =0.6658\approx 0.666~A/m^2~(Answer)\] (c) \(J_a\) has the maximum value near the surface of the wire.

7. [14] A human being can be electrocuted if a current as small as 50 mA passes near the heart. An electrician working with sweaty hands makes good contact with the two conductors he is holding, one in each hand. If his resistance is 2000 \(\Omega\), what might the fatal voltage be?

Solution:

\[V = iR = (50 \times 10^{-3}~A)(2000\Omega)=100~V~(Answer)\]

8. [17] A wire of Nichrome (a nickel–chromium–iron alloy commonly used in heating elements) is 1.0 m long and 1.0 \(mm^2\) in cross-sectional area. It carries a current of 4.0 A when a 2.0 V potential difference is applied between its ends. Calculate the conductivity \(\sigma\) of Nichrome.

Solution: \[R=\frac{V}{i}=\frac{2.0~V}{4.0~A}=0.5~\Omega\] \[\sigma = \frac{L}{RA}=\frac{1.0~m}{(0.5~\Omega)(1.0\times 10^{-6}~m^2)}=2.0\times 10^6~(\Omega.m)^{-1}~(Answer)\]

9. [19] What is the resistivity of a wire of 1.0 mm diameter, 2.0 m length, and 50 \(m\Omega\) resistance?

Solution: \[\rho = \frac{RA}{L} = \frac{(50\times 10^{-3}\Omega)(\pi (0.5\times 10^{-3}~m)^2)}{2.0~m}=1.96\times 10^{-8}~\Omega.m~(Answer)\]

10. [21] A common flashlight bulb is rated at 0.30 A and 2.9 V (the values of the current and voltage under operating conditions). If the resistance of the tungsten bulb filament at room temperature \((20^\circ ~C)\) is 1.1 \(\Omega\), what is the temperature of the filament when the bulb is on?

Solution: Resistance of the flashlight bulb under operating condition is \(R = \frac{V}{i}=\frac{2.9~V}{0.30~A}=9.67~\Omega\)

We know \(R = R_0(1+\alpha\Delta T)\), where \(\alpha = 4.5\times 10^{-3}~(1/K)\) is the temperature coefficient of tungsten as taken from Table 6-1.

\[T = \frac{R-R_0}{R_0\alpha}+T_0 = \frac{R-R_0}{R_0\alpha}+T_0=\frac{9.67~\Omega-1.1 \Omega}{(1.1 \Omega) (4.5\times 10^{-3}~(1/K)}+(20^\circ ~C)=1751.31~K~(Answer)\]

11. [22] Kiting during a storm. The legend that Benjamin Franklin flew a kite as a storm approached is only a legend—he was neither stupid nor suicidal. Suppose a kite string of radius 2.00 mm extends directly upward by 0.800 km and is coated with a 0.500 mm layer of water having resistivity 150 \(\Omega.m\). If the potential difference between the two ends of the string is 160 MV, what is the current through the water layer? The danger is not this current but the chance that the string draws a lightning strike, which can have a current as large as 500000 A (way beyond just being lethal).

Solution:

Resistance of the wet string is \(R = \frac{\rho L}{A}\), where the cross sectional area of the thin water layer is \[A = \pi (r+t)^2-\pi r^2\]

\[A = \pi (2.00\times 10^{-3}~m+0.500\times 10^{-3}~m)^2-\pi (2.00\times 10^{-3}~m^2)^2=7.06\times 10^{-6}~m^2\] \[R = \frac{\rho L}{A}=\frac{(150 ~\Omega.m)(0.800\times 10^3 ~m)}{7.06\times 10^{-6}~m^2}=16.997\times 10^9~\Omega\] Current through the water layer is \[i =\frac{V}{R}=\frac{160 ~\times 10^6~V}{16.997\times 10^9~\Omega}=9.41\times 10^{-3}~A~(Answer)\]

12. [24] Figure 6-7a gives the magnitude E(x) of the electric fields that have been set up by a battery along a resistive rod of length 9.00 mm (Fig. 6-7b).The vertical scale is set by \(E_s = 4.00 \times 10^3\) V/m. The rod consists of three sections of the same material but with different radii. (The schematic diagram of Fig. 6-7b does not indicate the different radii.) The radius of section 3 is 2.00 mm. What is the radius of (a) section 1 and (b) section 2?

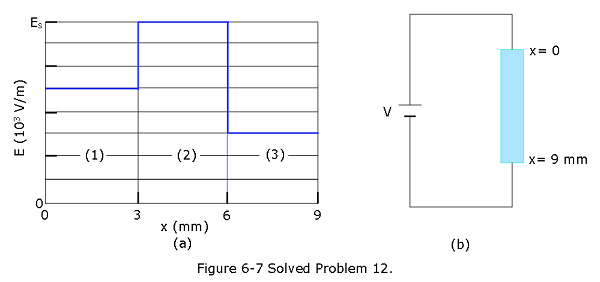
Solution:

In the given problem the rod consists of three sections of the same material (same resistivity \(\rho\)) but with different radii. The relation that holds between the sections as follows:

\[J_1A_1 = J_2A_2 = J_3A_3\] \[\frac{E_1}{\rho}\pi r_1^2 = \frac{E_2}{\rho}\pi r_2^2 =\frac{E_3}{\rho}\pi r_3^2\] \[E_1r_1^2 = E_2r_2^2 =E_3r_3^2\] \[(2.5\times 10^3~V/m)r_1^2 = (4.0\times 10^3~V/m)r_2^2 =(1.5\times 10^3~V/m)r_3^2\] (a) Radius of section 1 is: \[r_1 = \sqrt{\frac{1.5}{2.5}r_3^2}=\sqrt{\frac{1.5}{2.5}(2.0\times 10^{-3}~m)^2}=1.55\times 10^{-3}~m~=1.55~mm~(Answer)\]

2. Radius of section 2 is: \[r_2 = \sqrt{\frac{1.5}{4.0}r_3^2}=\sqrt{\frac{1.5}{4.0}(2.0\times 10^{-3}~m)^2}=1.22\times 10^{-3}~m~=1.22~mm~(Answer)\]

13. [34] Figure 6-8 shows wire section 1 of diameter \(D_1\) = 4.00R and wire section 2 of diameter \(D_2\) = 2.00R, connected by a tapered section. The wire is copper and carries a current. Assume that the current is uniformly distributed across any cross-sectional area through the wire’s width.The electric potential change V along the length L = 2.00 m shown in section 2 is 10.0 \(\mu V\). The number of charge carriers per unit volume is \(8.49 \times 10^{28} m^{-3}\). What is the drift speed of the conduction electrons in section 1?

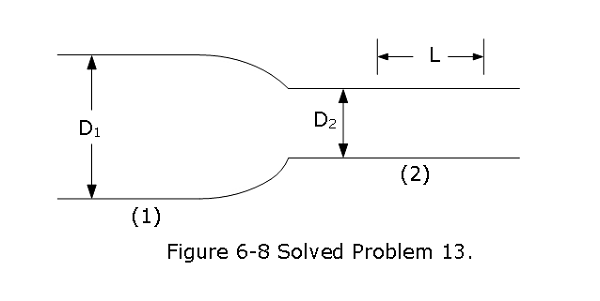
Solution:

According to the problem, the current passing through the two sections are equal, that leads to \[J_1A_1=J_2A_2\] \[J_1=J_2\frac{A_2}{A_1}=J_2\frac{\pi R^2}{4\pi R^2}=\frac{E}{\rho}\frac{\pi R^2}{4\pi R^2}=\frac{(V/L)}{\rho}\frac{1}{4}\] \[J_1=\frac{(V/L)}{\rho}\frac{1}{4}=\frac{V}{4L\rho}=\frac{10\times 10^{-6}~V}{4\times2.0~m\times 1.69\times 10^{-8}~\Omega.m}=73.96~A/m^2\approx74~A/m^2\] The drift speed of the conduction electrons in section 1 is:

\[v_d = \frac{J_1}{ne}=\frac{74~A/m^2}{(8.49\times 10^{28}/m^3)(1.6\times 10^{-19}~C)}=5.45\times 10^{-9}~m/s~(Answer)\]

14. [42] In Fig. 6-9, a battery of potential difference V = 12 V is connected to a resistive strip of resistance R = 6.0 \(\Omega\). When an electron moves through the strip from one end to the other, (a) in which direction in the figure does the electron move, (b) how much work is done on the electron by the electric field in the strip, and (c) how much energy is transferred to the thermal energy of the strip by the electron?

1. Electric field will be directed downwards and as a result the electrons will move in the upward direction.
2. Work done on the electron by the electric field in the strip: \(W = eV = (1.6\times 10^{-19}~C)(12~V)=19.60\times 10^{-19}~J~(Answer)\)$
3. Thermal energy transferred: The answer is same as (b) \(19.60\times 10^{-19}~J~(Answer)\)

15. [49] A 100 W lightbulb is plugged into a standard 120 V outlet. (a) How much does it cost per 31-day month to leave the light turned on continuously? Assume electrical energy costs US$0.06/kW.h. (b) What is the resistance of the bulb? (c) What is the current in the bulb?

Solution: (a) Electrical energy consumed for the 31-day month is \[E = P\Delta t = (100~W)(31~dys)\frac{24~hrs}{1~dy}=74.40~kW.h\] To cost comes out to be: \[Cost = (74.40~kW.h)(US\$0.06/kW.h)=\$4.46~(Answer)\]

2. Resistance of the bulb: \(R = \frac{V^2}{P}=\frac{(120~V)^2}{100~W}=144~\Omega~(Answer)\)
3. Current in the bulb: \(i = \frac{P}{V}=\frac{100~W}{120~V}=0.833~A~(Answer)\)

Problems Current & Resistance

Section 6-1 Electric Current

1. [2] An isolated conducting sphere has a 10 cm radius. One wire carries a current of 1.000 002 0 A into it. Another wire carries a current of 1.000 000 0 A out of it. How long would it take for the sphere to increase in potential by 1000 V?

Section 6-2 Current Density

2. [5] A beam contains \(2.0 \times 10^8\) doubly charged positive ions per cubic centimeter, all of which are moving north with a speed of \(1.0 \times 10^5\) m/s. What are the (a) magnitude and (b) direction of the current density (c) What additional quantity do you need to calculate the total current i in this ion beam?

3. [9] The magnitude J(r) of the current density in a certain cylindrical wire is given as a function of radial distance from the center of the wire’s cross section as J(r) = Br, where r is in meters, J is in amperes per square meter, and \(B = 2.00 \times 10^5~ A/m^3\). This function applies out to the wire’s radius of 2.00 mm. How much current is contained within the width of a thin ring concentric with the wire if the ring has a radial width of 10.0 mm and is at a radial distance of 1.20 mm?

4. [12] Near Earth, the density of protons in the solar wind (a stream of particles from the Sun) is 8.70 cm#3, and their speed is 470 km/s. (a) Find the current density of these protons. (b) If Earth’s magnetic field did not deflect the protons, what total current would Earth receive?

5. [13] How long does it take electrons to get from a car battery to the starting motor? Assume the current is 300 A and the electrons travel through a copper wire with cross-sectional area 0.21 \(cm^2\) and length 0.85 m. The number of charge carriers per unit volume is \(8.49 \times 10^{28} m^{-3}\).

Section 6-3 Resistance and Resistivity

6. [15] A coil is formed by winding 250 turns of insulated 16-gauge copper wire (diameter 1.3 mm) in a single layer on a cylindrical form of radius 12 cm. What is the resistance of the coil? Neglect the thickness of the insulation. (Use Table 6-1.)

7. [18] A wire 4.00 m long and 6.00 mm in diameter has a resistance of 15.0 m\(\Omega\). A potential difference of 23.0 V is applied between the ends. (a) What is the current in the wire? (b) What is the magnitude of the current density? (c) Calculate the resistivity of the wire material. (d) Using Table 26-1, identify the material.

8. [20] A certain wire has a resistance R.What is the resistance of a second wire, made of the same material, that is half as long and has half the diameter?

9. [23] When 115 V is applied across a wire that is 10 m long and has a 0.30 mm radius, the magnitude of the current density is \(1.4 \times 10^8~A/m^2\). Find the resistivity of the wire.

10. [28] Figure 26-27 gives the electric potential V(x) along a copper wire carrying uniform current, from a point of higher potential \(V_s = 12.0 \mu V\) at x = 0 to a point of zero potential at \(x_s = 3.00\) m. The wire has a radius of 2.00 mm. What is the current in the wire?

11. [35] In Fig. 26-30, current is set up through a truncated right circular cone of resistivity 731 \(\Omega.m\), left radius a 2.00 mm, right radius b = 2.30 mm, and length L = 1.94 cm. Assume that the current density is uniform across any cross section taken perpendicular to the length.What is the resistance of the cone?

Section 6-4 Ohm’s Law

12. [37] Show that, according to the free-electron model of electrical conduction in metals and classical physics, the resistivity of metals should be proportional to where T is the temperature in kelvins.

Section 6-5 Power, Semiconductors, Superconductors

13. [40] Thermal energy is produced in a resistor at a rate of 100 W when the current is 3.00 A.What is the resistance?

14. [41] A 120 V potential difference is applied to a space heater whose resistance is 14 when hot. (a) At what rate is electrical energy transferred to thermal energy? (b) What is the cost for 5.0 h at US$0.05/kW.h?