Lab-2 Discrete Time Signals
Name:Write down your name
Date: Date of report submission and date of lab performed
Implement the following using MATLAB:
Problem-1: Generate the following sequences using the following MATLAB signal functions and the basic MATLAB signal operations. Plot signal samples using the stem function:
- \(x(n)=3\delta(n+2)+2\delta(n)-\delta(n-3)+5\delta δ(n-7)\), \(-5 \le n \le 15\)
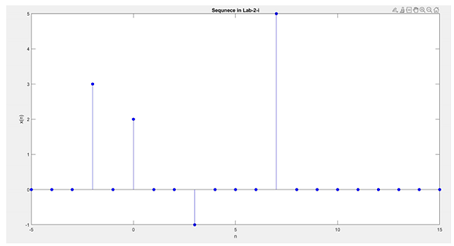
- \(x(n)= 5e^{(-0.1+j0.2n)},-10 \le n \le 10\)
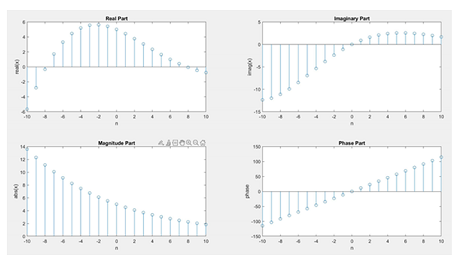
- \(x(n)=3sin(0.01\pi n)cos(0.5\pi n),-200 \le n\le 200\) Comment on the waveform shape.
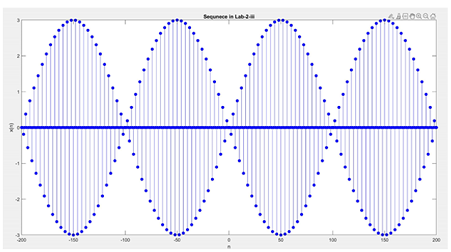
- \(x(n)=5[cos(0.49\pi n)+cos(0.51\pi n)],-200 \le n \le 200.\) Comment on the waveform shape.
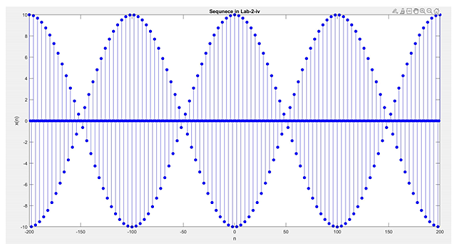
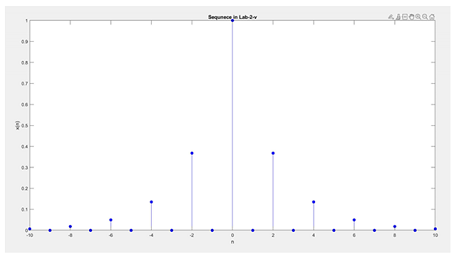
- \(x(n)=\displaystyle \sum_{k=-5}^5 e^{-|k|}\delta (n-2k)\), \(-10 \le n \le 10\)
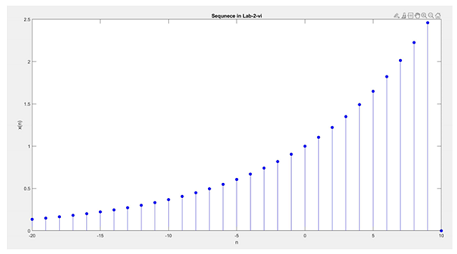
- \(x(n)=e^{0.1n}[u(n+20)-u(n-10)\)
Lab Report: Submit a lab report with your name and ID number. Report must include the MATLAB codes, output figures and the relevant discussion.
Useful MATLAB Codes:
%——————————————–
function [x,n] = stepseq(n0,n1,n2)
% Generates x(n) = u(n-n0); n1 <= n <= n2
% [x,n]= stepseq(n0,n1,n2)
% n = [n1:n2];
x = [(n-n0) >= 0];
%——————————————–
function [x,n] = impseq(n0,n1,n2)
% Generates x(n) = delta(n-n0); n1 <= n <= n2
% [x,n] = impseq(n0,n1,n2)
%
n = [n1:n2]; x = [(n-n0) == 0];
%——————————————–
function [y,n] = sigshift(x,m,k)
% Implements y(n) = x(n-k)
%————————————
% [y,n] = sigshift(x,m,k)
%
n = m + k; y = x;
%————————————
function [y,n] = sigmult(x1,n1,x2,n2)
% Implements y(n) = x1(n)*x2(n)
%————————————————
% [y,n] =sigmult(x1,n1,x2,n2)
% y = product sequence over n, which includes n1 and n2
% x1 = first sequence over n1
% x2 = second sequence over n2 (n2 can be different from n1)
n = min(min(n1),min(n2)):max(max(n1),max(n2)); %
Duration of y(n)
y1 = zeros(1,length(n)); y2 = y1; %Initialization
y1(find((n >= min(n1)) & (n <= max(n1)) == 1)) =
x1; % x1 with duration of y
y2(find((n >= min(n2)) & (n <= max(n2)) == 1)) =
x2; % x2 with duration of y
y = y1.*y2;
% Sequence multiplication
%—————————————–
function [y,n] = sigfold(x,n)
% Implements y(n) = x(-n)
%—————————–
% [y,n] = sigfold(x,n)
%
y = fliplr(x); n = -fliplr(n);
%—————————–
function [y,n] = sigadd(x1,n1,x2,n2)
% Implements y(n) = x1(n) + x2(n)
%————————————————
% [y,n] = sigadd(x1,n1,x2,n2)
% y = sum sequence over n, which includes n1 and n2
% x1 = first sequence over n1
% x2 = second sequence over n2 (n2 can be different from n1)
n = min(min(n1),min(n2)):max(max(n1),max(n2)); % Duration of y(n)
y1 = zeros(1,length(n)); y2 = y1; %Initialization
y1(find((n>= min(n1)) & (n<=max(n1)) == 1)) = x1;
% x1 with duration of y
y2(find((n>= min(n2)) & (n<=max(n2)) == 1)) = x2;
% x2 with duration of y
y = y1+y2;
% Sequence addition
%——————————————-
function[xe,xo,n] = evenodd(x,n)
% Real signal decomposition into even and odd parts
% ——————————————-
% [xe, xo, m] = evenodd(x,n)
%
if any (imag(x) ~= 0) error(‘x is not a real sequence’) end
m = -fliplr(n);
m1 = min([m,n]); m2 = max([m,n]); m = m1:m2;
nm = n(1)-m(1); n1 = 1:length(n);
x1 = zeros(1,length(m)); x1(n1+nm) = x; x = x1;
xe = 0.5*(x+fliplr(x));
xo = 0.5*(x-fliplr(x));
% —————————————–
function [y,ny] = conv_m(x,nx,h,nh)
% Modified convolution routine for signal processing
% —————————————–
% [y,ny] = conv_m(x,nx,h,nh)
% [y,ny] = convolution result
% [x,nx] = first signal
% [h,nh] = second signal
%
nyb = nx(1) + nh(1);
nye = nx(length(x)) + nh(length(h));
ny = [nyb:nye]; y = conv(x,h);
% ———————————————