Chapter 4 Motion in Two and Three Dimensions

Learning Objectives:

In this chapter you will basically learn:

\(\bullet\) Learn how to draw a position vector locating a point in two-dimensional and three-dimensional coordinate system indicating the components along the axes of a coordinate system.

\(\bullet\) Learn how to determine the direction and magnitude of a particle’s position vector from its components.

\(\bullet\) Learn how in magnitude-angle and unit-vector notations, and knowing the particle’s initial and final position vectors, the time interval between those positions, how to calculate the particle’s average velocity vector. Also, given a particle’s position vector as a function of time, learn how to determine instantaneous velocity of a particle.

\(\bullet\) Learn with the given the initial and final velocity vectors of a particle and the time interval between those velocities, determine the average acceleration vector in magnitude-angle and unit-vector notations.

\(\bullet\) Learn with the given particle’s velocity vector as a function of time, how to determine its (instantaneous) acceleration vector.

\(\bullet\) Learn how the magnitudes and directions of the velocity and acceleration components during the flight of a projectile motion without and with air resistance.

\(\bullet\) Learn with the given launch velocity in either magnitude-angle or unit-vector notation, how to calculate the particle’s position, displacement, and velocity at a given instant during the flight.

\(\bullet\) Learn uniform circular motion and explain the velocity and acceleration vectors (magnitude and direction) during the motion.

\(\bullet\) Learn how the radius of the circular path, the period, the particle’s speed, and the particle’s acceleration magnitude are related.

\(\bullet\) Learn the relationship between a particle’s position, velocity, and acceleration as measured from two reference frames that move relative to each other at constant velocity and along a single axis.

4.1 Position and Displacement:

A particle (or particle-like object) can be located in a three dimensional space by a position vector \(\vec r\), which is a vector that extends from a reference point (usually the origin) to the particle. In the unit-vector notation position vector \(\vec r\) can be written in a cartesian coordinate system as

\[\begin{equation} \vec r = x \hat i + y \hat j + z \hat k \tag{4.1} \end{equation}\]

where \(x\hat i\) , \(y\hat j\) , and \(z\hat k\) are the vector components and the coefficients x, y, and z are its scalar components.

The coefficients x, y, and z give the particle’s location along the coordinate axes and relative to the origin; that is, the particle has the rectangular coordinates (x, y, z). For instance, Fig. 4-1 shows a particle with position vector

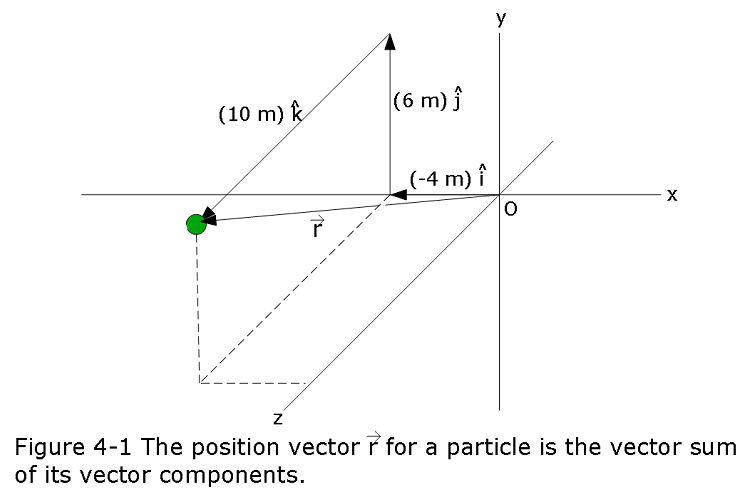
\[\begin{equation} \vec r = (-4 m) \hat i + (6 m) \hat j + (10 m) \hat k \end{equation}\]

and rectangular coordinates (-4 m, 6 m, 10 m). Along the x axis the particle is 4 m from the origin, in the \(-\hat i\) direction. Along the y axis it is 6 m from the origin, in the \(+\hat j\) direction. Along the z axis it is 10 m from the origin, in the \(+\hat k\) direction.

As the particle changes its position vector, from \(\vec r_1\)to \(\vec r_2\) during a certain time interval \(\Delta t\) then the particle’s displacement \(\Delta \vec r\) during that time interval \(\Delta t\) is

\[\begin{equation} \Delta\vec r=\vec r_2-\vec r_1 \tag{4.2} \end{equation}\]

Using the unit-vector notation of Eq. 4-1, we can rewrite this displacement as

\[\begin{equation} \Delta\vec r=(x_2 \hat i + y_2 \hat j + z_2 \hat k)-(x_1 \hat i + y_1 \hat j + z_1 \hat k) \end{equation}\]

or

\[\begin{equation} \Delta\vec r=(x_2 - x_1)\hat i + (y_2 -y_1)\hat j + (z_2 - z_1)\hat k \tag{4.3} \end{equation}\]

where coordinates \((x_1, y_1, z_1)\) correspond to position vector and coordinates \((x_2, y_2, z_2)\) correspond to position vector \(\vec r\). We can also rewrite the displacement by substituting \(\Delta x\) for \((x_2 - x_1)\), \(\Delta y\) for \((y_2 - y_1)\), and \(\Delta z\) for \((z_2 - z_1)\):

\[\begin{equation} \Delta\vec r=\Delta x\hat i + \Delta y\hat j + \Delta z\hat k \tag{4.4} \end{equation}\]

4.2 Average and Instantaneous Velocity:

Unlike we discussed average and instantaneous velocities in Chapter-2, we need to use vector quantities to describe the displacement \(\Delta r\) of a particle in a time interval \(\Delta t\), then its average velocity is

\[\begin{equation} average~velocity=\frac{displacement}{time~ interval}, \end{equation}\] or

\[\begin{equation} \vec v_{avg}=\frac{\Delta \vec r}{\Delta t}. \tag{4.5} \end{equation}\]

In terms of vector components the Eq. 4-5 can be written as

\[\begin{equation} \vec v_{avg}=\frac{\Delta x\hat i + \Delta y\hat j + \Delta z\hat k}{\Delta t}=\frac{\Delta x}{\Delta t}\hat i + \frac{\Delta y}{\Delta t}\hat j + \frac{\Delta z}{\Delta t}\hat k. \tag{4.6} \end{equation}\]

The instantaneous velocity of particle at a particular instant when the value of time interval $t $approaches in the limit to 0 at that particular instant is given by:

\[\begin{equation} \vec v = \lim_{\Delta t \to 0}\frac{\Delta \vec r}{\Delta t}=\frac{d\vec r}{dt}=\frac{dx}{dt}\hat i+\frac{dy}{dt}\hat j + \frac{dz}{dt}\hat k=v_x\hat i+v_y \hat j+v_z\hat k. \tag{4.7} \end{equation}\]

where the scalar components of the instantaneous velocity \(\vec v\) are

\[\begin{equation} v_x = \frac{dx}{dt}, v_y = \frac{dy}{dt}, ~and ~v_z= \frac{dz}{dt} \tag{4.8} \end{equation}\]

The direction of the instantaneous velocity of a particle is always tangent to the particle’s path at the particle’s position.

4.3 Average and Instantaneous Acceleration:

When a particle’s velocity changes from \(\vec v_1\) to \(\vec v_2\) in a time interval \(\Delta t\), its average acceleration \(\vec a_{avg}\) during \(\Delta t\) is

\[\begin{equation} \vec a_{avg}=\frac{\vec v_2-\vec v_1}{\Delta t}=\frac{\Delta \vec v}{\Delta t}. \tag{4.9} \end{equation}\]

The instantaneous acceleration of particle at a particular instant when the value of time interval $t $approaches in the limit to 0 at that particular instant is given by:

\[\begin{equation} \vec a = \lim_{\Delta t \to 0}\frac{\Delta \vec v}{\Delta t}=\frac{d\vec v}{dt}=\frac{dv_x}{dt}\hat i+\frac{dv_y}{dt}\hat j + \frac{dv_z}{dt}\hat k=a_x\hat i+a_y \hat j+a_z\hat k. \tag{4.10} \end{equation}\]

where the scalar components of the instantaneous acceleration \(\vec a\) are

\[\begin{equation} a_x = \frac{dv_x}{dt}, a_y = \frac{dv_y}{dt}, ~and ~a_z= \frac{dv_z}{dt} \tag{4.11} \end{equation}\]

4.4 Projectile Motion, Uniform Circular Motion:

A particle moves in a two-dimensional motion with vertical plane with some initial velocity but its acceleration is always the freefall acceleration \(\vec g\), which is downward. The motion is called a projectile motion.

The projectile is launched with an initial velocity \(\vec v_0\) that can be written as

\[\begin{equation} \vec v_0=v_{0x}\hat i+\vec v_{0y}\hat j \tag{4.12} \end{equation}\]

The components \(v_{0x}\) and \(v_{0y}\) can then be found if we know the angle \(\theta_0\) between \(\vec v_0\) and the positive x direction:

\[\begin{equation} v_{0x}=v_0\cos\theta_0~~~~~and~~~~~ v_{0y}=v_0\sin\theta_0 \tag{4.13} \end{equation}\]

In the two-dimensional motion as shown in Fig. 4-2, the projectile’s position vector \(\vec r\) and velocity vector \(\vec v\) change continuously, but its acceleration vector \(\vec a\) is constant and always directed vertically downward.The projectile has no horizontal acceleration.

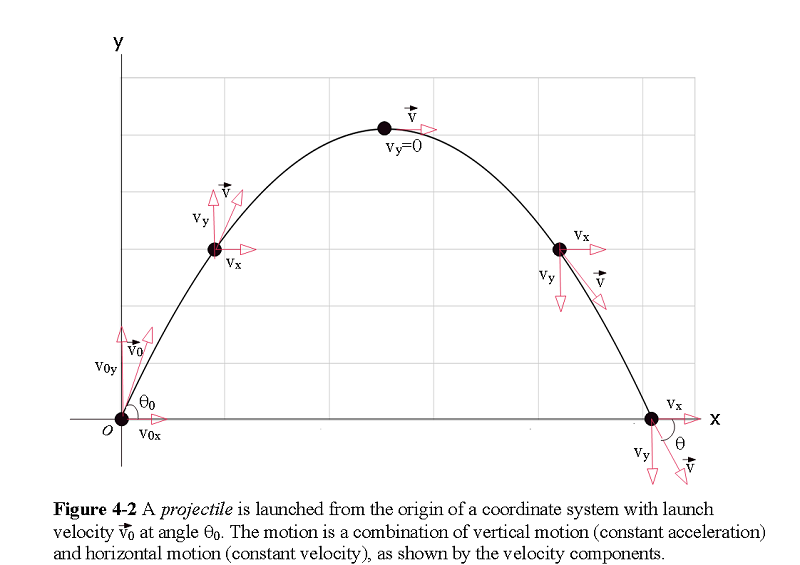
There is no acceleration in the horizontal direction, the horizontal component \(v_x\) of the projectile’s velocity remains unchanged from its initial value \(v_{0x}\) throughout the motion, as shown in Fig. 4-12. At any time t, the projectile’s horizontal displacement \(x- x_0\) from an initial position \(x_0\) is given by Eq. 2-11 with \(a=0\), which we write as

\[\begin{equation} x - x_{0} = v_{0x}t=(v_0cos\theta_0)t \tag{4.14} \end{equation}\]

The vertical motion is the motion for a particle in free fall. Most important is that the acceleration is constant. Thus, the equations of Table 2-1 apply, provided we substitute -g for a and switch to y notation.Then, for example, Eq. 2-11 becomes

\[\begin{equation} y - y_{0} = v_{0y}t-\frac{1}{2}gt^2=(v_0sin\theta_0)t-\frac{1}{2}gt^2 \tag{4.15} \end{equation}\]

\[\begin{equation} v_y = v_0sin\theta_0-gt \tag{4.16} \end{equation}\]

\[\begin{equation} v_y^2 = (v_0sin\theta_0)^2-2g(y-y_0) \tag{4.17} \end{equation}\]

Equation Number	Equation
\(4-14\)	\(x-x_0 = (v_0cos\theta_0)t ~ ~ Horizontal~Motion\)
\(4-15\)	\(y-y_0 = (v_0sin\theta_0)t-\frac{1}{2}gt^2~~Vertical~Motion\)
\(4-16\)	\(v_y = (v_0sin\theta_0)-gt~~Vertical~Motion\)
\(4-17\)	\(v_y^2 = (v_0sin\theta_0)^2-2g(y-y_0)~~ Vertical~Motion\)

Projectile motion is a parabolic motion. We can substiture t from Eqn 4-14 to 4-15, and after some algebra we can find the following parabolic equation:

\[\begin{equation} y = (tan\theta_0)x-\frac{gx^2}{2(v_0cos\theta_0)^2} \tag{4.18} \end{equation}\]

Eqn. 4-18, is a parabolic equation, \[y=ax + bx^2\]

with \(a=tan\theta_0\) and \(b = -\frac{g}{2(v_0cos\theta_0)^2}\).

4.5 Horizontal Range:

The horizontal range R of the projectile is the maximum horizontal distance that the projectile travels when it returns to its initial height (the height at which it is launched). To find range R, we let \(x-x_0=R\) in Eq. 4-14 and \(y-y_0\) in Eq. 4-15, we get

\[R = (v_0~cos\theta_0)t\] \[0 = (v_0sin\theta_0)t-\frac{1}{2}gt^2\] Elimating from t from the above equations, we get

\[\begin{equation} R = \frac{2v_0^2}{g}sin\theta_0~cos\theta_0 = \frac{v_0^2}{g}sin2\theta_0 \tag{4.19} \end{equation}\]

Example Problem 4-1 A projectile is thrown with an initial velocity \(v_0= 100~m/s\), and an initial angle \(\theta_0=30^\circ.\) Find the (a) horizontal range, (b) maximum height attained by the projectile, and (c) time of flight of the projectile before it hits the ground.

Solution: (a) Using Eq. 4-19, the horizontal range, \[R=\frac{v_0^2\sin 2\theta}{g}=\frac{(100~m/s)^2\sin(2\times \pi\times 30^\circ/180^\circ)}{9.8~m/s^2}=882.80~m\]

2. Letting \(v_y=0\) in Eq. 4-17, we get the formula to calculate the maximum height attained by the projectile.

\[H=\frac{2v_0\sin\theta}{g}=(\frac{2\times 100~m/s)\sin(2\times \pi\times 30^\circ/180^\circ)}{9.8~m/s^2}=127.42~m\]

3. Time of flight: \(t=\frac{v_0\sin\theta}{g}=\frac{(100~m/s)\sin(2\times \pi\times 30^\circ/180^\circ)}{9.8~m/s^2}=10.19~s\)

4.6 Uniform Circular Motion:

A particle is in uniform circular motion if it travels around a circle or a circular arc at constant (uniform) speed. Although the speed does not vary, the particle is accelerating because the velocity changes in direction as can be seen in Figure 4-3.

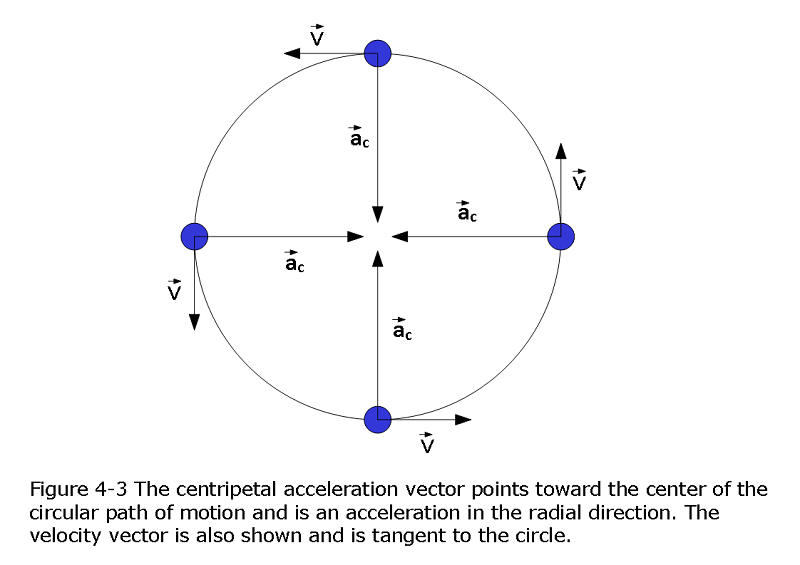
The acceleration associated with uniform circular motion is called a centripetal (meaning “center seeking”) acceleration. The magnitude of this acceleration \(\vec a\) is

\[\begin{equation} a = \frac{v^2}{r} \tag{4.20} \end{equation}\]

where r is the radius of the circle and v is the speed of the particle. During this accelerating motion at constant speed, the particle travels the circumference of the circle (a distance of \(2\pi r\)) in time

\[\begin{equation} T = \frac{2\pi r}{v}~~(Time-period) \tag{4.21} \end{equation}\]

T is called the period of revolution, or simply the period, of the motion.

Example Problem 4.2 A jet is flying at 150 m/s along a straight line and makes a turn along a circular path level with the ground. What does the radius of the circle have to be to produce a centripetal acceleration of 1 g on the pilot and jet toward the center of the circular trajectory?

Solution:

Using Eq. 4-20, we set the centripetal acceleration equal to the acceleration of gravity: \(9.8~m/s^2=v^2/r\).

Solving for the radius, we find

r= \(\frac{(150~m/s)^2}{9.8~m/s^2}= 2,295.91~m/s = 2.296~km.\space(Answer)\)

Analysis: It is important not to create a greater acceleration than g on the pilot, as well as for the passengers. To create a greater acceleration the pilot has to either decrease the radius of its circular trajectory or increase its speed on its existing trajectory or both.

4.7 Projectile Motion with Air Resistance (Research):

Suppose that a projectile of mass \(m\) is launched, at \(t=0\), from ground level (in a flat plain), making an angle \(\theta\) to the horizontal. Let’s consider that, in addition to the force of gravity, the projectile is subjected to air resistance acting in the opposite direction to its instantaneous direction of motion, and whose magnitude is directly proportional to its instantaneous speed. This is not a particularly accurate model of the drag force due to air resistance (the magnitude of the drag force is typically proportion to the square of the speed). However, with this model we can, at least, get some idea of how air resistance modifies projectile trajectories.

Let us adopt a Cartesian coordinate system whose origin coincides with the launch point, and whose \(y\)-axis points vertically upward. Let the initial velocity of the projectile lie in the \(x\)-\(y\) plane. Note that, since neither gravity nor the drag force cause the projectile to move out of the \(x\)-\(y\) plane, we can ignore the \(z\) coordinate in this problem.

The equation of motion of our projectile is written

\[\begin{equation} m\frac{d{\bf v}}{dt} = m{\bf g} - c{\bf v} \tag{4.22} \end{equation}\]

where \({\bf v} = (v_x, v_y)\) is the projectile velocity, \({\bf g} = (0, -g)\) the acceleration due to gravity, and \(c\) is a positive constant. In component form, the above equation becomes

\(\frac{dv_x}{dt}=-\frac{cv_x}{m}=- g\frac{v_x}{v_t},\) \(\frac{dv_y}{dt}=-g-\frac{cv_y}{m}=- g\left(1+\frac{v_y}{v_t}\right).\)

Here, we assumded \(v_t = mg/c\) is the terminal velocity. The velocity at which the drag force balances the gravitational force (for a projectile falling vertically downward).

Integrating x-component of the equation, we obtain \[\begin{equation} \int_{v_{x0}}^{v_x}\frac{d v_x}{v_x} = -\int_0^t\frac{g}{v_t}dt, \tag{4.23} \end{equation}\]

where \(v_{x0} = v_0\cos\theta\) is the \(x\)-component of the launch velocity. Hence,

\[\begin{equation} \ln\left(\frac{v_x}{v_{x\,0}}\right) = - \frac{g}{v_t}\,t, \tag{4.24} \end{equation}\]

or

\[\begin{equation} v_x = v_0\,\cos\theta\,{\rm e}^{-g\,t/v_t} \tag{4.25} \end{equation}\]

It is clear, from the above equation, that air drag causes the projectile’s horizontal velocity, which would otherwise be constant, to decay exponentially on a time-scale of order \(v_t/g\).

Integrating y-component of equation, we get

\[\begin{equation} \int_{v_{y0}}^{v_y} \frac{dv_y}{v_t+v_y} = - \int_0^t\frac{g}{v_t}\,t, \tag{4.26} \end{equation}\]

where \(v_{y0}=v_0\,\sin\theta\) is the \(y\)-component of the launch velocity. Hence,

\[\begin{equation} \ln\left(\frac{v_t+v_y}{v_t+v_{y0}}\right) = - \frac{g}{v_t}\,t, \tag{4.27} \end{equation}\]

or \[\begin{equation} v_y = v_0\,\sin\theta\,{\rm e}^{-g\,t/v_t} - v_t\left(1-e^{-g\,t/v_t}\right) \tag{4.28} \end{equation}\]

It thus follows, from Equations () and (), that if the projectile stays in the air much longer than a time of order \(v_t/g\) then it ends up falling vertically downward at the terminal velocity, \(v_t\), irrespective of its initial launch angle.

Integrating Eq. 4-12 yields

\[\begin{equation} \int_{0}^{x}dx = \int_0^t(v_0\cos\theta)e^{-\frac{gt}{v_t}}dt, \tag{4.29} \end{equation}\]

\[\begin{equation} x = \frac{v_0\,v_t\cos\theta}{g}\left(1-{\rm e}^{-g\,t/v_t}\right) \tag{4.30} \end{equation}\]

In the limit \(t\ll v_t/g\), the above equation can be expanded Binomially to reduce to

\[\begin{equation} x = v_0(\cos\theta)t, \tag{4.31} \end{equation}\]

which is the standard result in the absence of air drag. In the opposite limit, \(t\gg v_t/g\), we get

\[\begin{equation} x = \frac{v_0\,v_t\,\cos\theta}{g} \tag{4.32} \end{equation}\]

The above expression clearly sets an effective upper limit on how far the projectile can travel in the horizontal direction. Integrating Eq. 4-14 gives

\[\begin{equation} \int_{0}^{y}dy = \int_0^t\left[v_0\,\sin\theta\,{\rm e}^{-g\,t/v_t} - v_t\left(1-e^{-g\,t/v_t}\right)\right] dt, \tag{4.33} \end{equation}\]

\[\begin{equation} y = \frac{v_t}{g}\,\left(v_0\,\sin\theta + v_t\right)\left(1-{\rm e}^{-g\,t/v_t}\right) - v_t\,t. \tag{4.34} \end{equation}\]

In the limit \(t\ll v_t/g\), this equation reduces to

\[\begin{equation} y = v_0\,\sin\theta\,t - \frac{g}{2}\,t^2 \tag{4.35} \end{equation}\]

which is the standard result in the absence of air drag. In the opposite limit, \(t\gg v_t/g\), we get

\[\begin{equation} y = \frac{v_t}{g}\,\left(v_0\,\sin\theta + v_t\right) - v_t\,t \tag{4.36} \end{equation}\]

Incidentally, the above analysis implies that air resistance only starts to have an appreciable effect on the trajectory after the projectile has been in the air a time of order \(v_t/g\).

It is clear, from the previous two equations, that the time of flight of the projectile (i.e., the time at which \(y=0\), excluding the trivial result \(t=0\)) is

\[\begin{equation} t_f = \frac{2\,v_0\,\sin\theta}{g} \tag{4.37} \end{equation}\]

when \(t\ll v_t/g\), which implies that \(v_0\,\sin\theta \ll v_t\), and

\[\begin{equation} t_f = \frac{v_0\,\sin\theta}{g} \tag{4.38} \end{equation}\]

when \(t\gg v_t/g\), which implies that \(v_0\,\sin\theta \gg v_t\) (i.e., the vertical component of the launch velocity is much greater than the terminal velocity). It thus follows, from Equations () and (), that the horizontal range [i.e., \(x(t_f)\)] of the projectile is

\[\begin{equation} R = \frac{v_0^{\,2}\,\sin(2\,\theta)}{g} \tag{4.39} \end{equation}\]

when \(v_0\,\sin\theta \ll v_t\), and

\[\begin{equation} R= \frac{v_0\,v_t\,\cos\theta}{g} \tag{4.40} \end{equation}\]

when \(v_0\,\sin\theta \gg v_t\). Equation (4-23) is, of course, the standard result without air resistance. This result implies that, in the absence of air resistance, the maximum horizontal range, \(v_0^{\,2}/g\), is achieved when the launch angle \(\theta\) takes the value \(45^\circ\). On the other hand, Equation () implies that, in the presence of air resistance, the maximum horizontal range, \(v_0\,v_t/g\), is achieved when \(\theta\) is made as small as possible.

However, \(\theta\) cannot be made too small, since expression (4-24) is only valid when \(v_0\sin\theta \gg v_t\). In fact, assuming that \(v_0\gg v_t\), the maximum horizontal range, \(v_0\,v_t/g\), is achieved when \(\theta\sim v_t/v_0\ll 1\). We thus conclude that if air resistance is significant then it causes the horizontal range of the projectile to scale linearly, rather than quadratically, with the launch velocity, $v_0 $. Moreover, the maximum horizontal range is achieved with a launch angle which is much shallower than the standard result, \(45^\circ\).

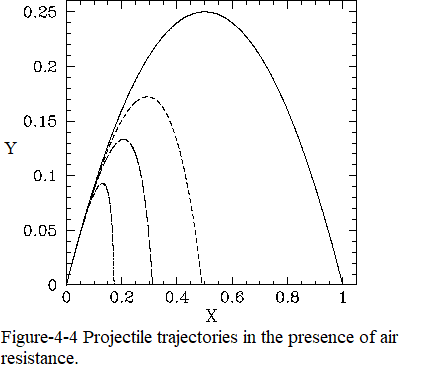
Figure-4-4 shows some example trajectories calculated, from the above model, with the same launch angle, \(45^\circ\), but with different values of the ratio \(v_0/v_t\). Here, \(X=x/(v_0^{\,2}/g)\) and \(Y=y/(v_0^{\,2}/g)\). The solid, short-dashed, long-dashed, and dot-dashed curves correspond to \(v_0/v_t = 0\), \(1\), \(2\), and \(4\), respectively. It can be seen that as the air resistance strength increases (i.e., as \(v_0/v_t\) increases), the range of the projectile decreases. Furthermore, there is always an initial time interval during which the trajectory is identical to that calculated in the absence of air resistance (i.e., \(v_0/v_t = 0\)). Finally, in the presence of air resistance, the projectile tends to fall more steeply than it rises. Indeed, in the presence of strong air resistance (i.e., \(v_0/v_t=4\)), the projectile falls almost vertically.

4.8 Velocity Dependent Forces (Research):

Consider a particle of mass \(m\) moving in one dimension under the action of a force, \(f\), which is a function of the particle’s speed, \(v\), but not of its displacement, \(x\). Note that such a force is intrinsically non-conservative [since it clearly cannot be ex pressed as minus the gradient of some potential function, \(U(x)\)]. Now, the particle’s equation of motion is written

\[\begin{equation} m\,\frac{dv}{dt} = f(v) \tag{4.41} \end{equation}\]

Integrating this equation, we obtain

\[\begin{equation} \int_{v_0}^v \frac{dv'}{f(v')} = \frac{t}{m} \tag{4.42} \end{equation}\]

where \(v(t=0)=v_0\). In principle, the above equation can be solved to give \(v(t)\). The equation of motion is also written

\[\begin{equation} m\,v\,\frac{dv}{dx} = f(v) \tag{4.43} \end{equation}\]

since \(v=dx/dt\). Integrating this equation, we obtain

\[\begin{equation} \int_{v_0}^v \frac{v'\,dv'}{f(v')} = \frac{x-x_0}{m} \tag{4.44} \end{equation}\]

where \(x(t=0)=x_0\). In principle, the above equation can be solved to give \(v(x)\). Let us now consider a specific example. Suppose that an object of mass \(m\) falls vertically under gravity. Let \(x\) be the height through which the object has fallen since \(t=0\), at which time the object is assumed to be at rest. It follows that \(x_0=v_0=0\). Suppose that, in addition to the force of gravity, \(m\,g\), where \(g\) is the gravitational acceleration, our object is subject to a retarding air resistance force which is proportional to the square of its instantaneous velocity. The object’s equation of motion is thus

\[\begin{equation} m\,\frac{dv}{dt} = m\, g - c\,v^2 \tag{4.45} \end{equation}\]

where \(c>0\). This equation can be integrated to give

\[\begin{equation} \int_0^v \frac{dv'}{1-(v'/v_t)^2} = g\,t \tag{4.46} \end{equation}\]

where \(v_t=(m\,g/c)^{1/2}\). Making a change of variable, we obtain

\[\begin{equation} \int_0^{v/v_t}\frac{dy}{1-y^2} = \frac{g}{v_t}\,t \tag{4.47} \end{equation}\]

The left-hand side of the above equation is now a standard integral, which can be solved to give

\[\begin{equation} \tanh^{-1}\left(\frac{v}{v_t}\right) = \frac{g\,t}{v_t} \tag{4.48} \end{equation}\]

or

\[\begin{equation} v = v_t\,\tanh\left(\frac{g\,t}{v_t}\right) \tag{4.49} \end{equation}\]

Thus, when \(t\ll v_t/g\), we obtain the standard result \(v\simeq g\,t\), since \(\tanh x\simeq x\) for \(x\ll 1\). However, when \(t\gg v_t/g\), we get \(v\simeq v_t\), since \(\tanh x\simeq 1\) for \(x\gg 1\). It follows that air resistance prevents the downward velocity of our object from increasing indefinitely as it falls. Instead, at large times, the velocity asymptotically approaches the so-called terminal velocity, \(v_t\) (at which the gravitational and air resistance forces balance).

The equation of motion of our falling object is also written

\[\begin{equation} m\,v\,\frac{dv}{dx} = m\,g - c\,v^2 \tag{4.50} \end{equation}\]

This equation can be integrated to give

\[\begin{equation} \int_0^v\frac{v'\,dv'}{1-(v'/v_t)^2} = g\,x \tag{4.51} \end{equation}\]

Making a change of variable, we obtain

\[\begin{equation} \int_0^{(v/v_t)^2} \frac{dy}{1-y} = \frac{x}{x_t} \tag{4.52} \end{equation}\]

where \(x_t = m/ (2\,c)\). The left-hand side of the above equation is now a standard integral, which can be solved to give

\[\begin{equation} -\ln\!\left[1-\left(\frac{v}{v_t}\right)^2\right] = \frac{x}{x_t} \tag{4.53} \end{equation}\]

or

\[\begin{equation} v = v_t\left(1-{\rm e}^{-x/x_t}\right)^{1/2} \tag{4.54} \end{equation}\]

It follows that our object needs to fall a distance of order \(x_t\) before it achieves its terminal velocity.

Incidentally, it is quite easy to account for an air resistance force which scales as the square of projectile velocity. Let us imaging that our projectile is moving sufficiently rapidly that air does not have enough time to flow around it, and is instead simply knocked out of the way. If our projectile has cross-sectional area \(A\), perpendicular to the direction of its motion, and is moving with speed \(v\), then the mass of air that it knocks out of its way per second is \(\rho_a\,A\,v\), where \(\rho_a\) is the mass density of air. Suppose that the air knocked out of the way is pushed in the direction of the projectile’s motion with a speed of order \(v\). It follows that the air gains momentum per unit time \(\rho_a\,A\,v^2\) in the direction of the projectile’s motion. Hence, by Newton’s third law, the projectile loses the same momentum per unit time in the direction of its motion. In other words, the projectile is subject to a drag force of magnitude

\[\begin{equation} f_{drag} = C\,\rho_a\,A\,v^2 \tag{4.55} \end{equation}\]

acting in the opposite direction to its motion. Here, \(C\) is an \({\cal O}(1)\) dimensionless constant, known as the drag coefficient, which depends on the exact shape of the projectile. Obviously, streamlined projectiles, such as arrows, have small drag coefficients, whereas non-streamlined projectiles, such as bricks, have large drag coefficients. From before, the terminal velocity of our projectile is \(v_t=(m\,g/c)^{1/2}\), where \(m\) is its mass, and \(c=C\,\rho_a\,A\). Writing \(m = A\,d\,\rho\), where \(d\) is the typical linear dimension of the projectile, and \(\rho\) its mass density, we obtain

\[\begin{equation} v_t = \left(\frac{\rho\,g\,d}{\rho_a\,C}\right)^{1/2} \tag{4.56} \end{equation}\]

The above expression tells us that large, dense, streamlined projectiles (e.g., medicine balls) tend to have large terminal velocities, and small, rarefied, non-streamlined projectiles (e.g., feathers) tend to have small terminal velocities. Hence, the former type of projectile is relatively less affected by air resistance than the latter.

4.8.1 Python exercise for projectile motion (Research)

In this exercise, we will use a simple script to plot the trajectory of a projectile with inclusion of air resistance. We will also calculate the range of the projectile.

The air resistance drag force \(F_d\) in N is approximated by the following relation.

\[F_d = C_dv^2\]

Here, v is the magnitude of velocity in m/s and \(C_d\) is the coefficient of drag.

The following is a step-by-step guide to writing up the script. Some parts of the script have been left out for you to fill in.

Define the parameters in the problem First we import the modules we need: numpy to provide some mathematics functions, and matplotlib for plotting.

To start describing the problem, we need to define the parameters in the problem.

the mass of the projectile acceleration due to gravity initial velocity (magnitude and direction) drag coefficient We also set the time step to track the trajectory.

Set up the variables at time zero Next, we generate velocity of the projectile as a function of time. To do that, we create the following lists.

\(\bullet\) list to store the values of time t

\(\bullet\) ist to store x-component of velocity \(v_x\)

\(\bullet\) ist to store y-component of velocity \(v_y\)

\(\bullet\) ist to store x-component of acceleration \(a_x\)

\(\bullet\) ist to store y-component of acceleration \(a_y\)

We start by putting in the initial velocity components \(v_x = V\cos\theta\) and \(v_y=V\sin\theta\) at t=0

To get the acceleration, we need to find the resultant force, which consists of the air drag \(F_d\) and weight W = Mg

where \(\theta\) is the angle that the velocity forms with the positive x-axis. The force components follow the convention that they are positive when pointing to the right and upwards.

By Newton’s second law, the acceleration of the projectile is thus given by

\[F_d=C_dv^2\]

The x and y components of the resultant force are given by

\[F_x=-F_d\cos\theta\] and \[F_y=-Mg-F_d\sin\theta\]

Let’s implement these steps to get the velocity, drag force, and acceleration at t=0.

Update the velocity for every time-step

To get the velocity at the next time step, we make use of the following approximation.

\[a(t_n)=\frac{dv(t_n)}{dt}\approx\frac{v(t_{n+1})-v(t_n)}{\Delta t}\] or \[v(t_{n+1})\approx v(t_n)+a(t_n)\Delta t\]

This is just a very primitive way of doing integration of acceleration to get velocity. In the literature, this is known as Euler’s method.

Let us calculate 10 sets of velocities for 10 time-steps. We will use a while-loop and keep a counter to count to 10.

Update the positions

After we have obtained the velocities, we can get the xx and yy positions of the projectile using a similar concept.

\[v_x(t_n)=\frac{dx(t_n)}{dt}\approx \frac{x(t_{n+1})-x(t_n)}{\Delta t}\] \[v_y(t_n)=\frac{dy(t_n)}{dt}\approx \frac{y(t_{n+1})-y(t_n)}{\Delta t}\] or \[x(t_{n+1})\approx x(t_n)+v_x(t_n)\Delta t\] and \[y(t_{n+1})\approx y(t_n)+v_y(t_n)\Delta t\]

Starting with x=0x=0 and y=0 at t=0, we can use Euler’s method to get the positions for the 10 time-steps using the velocities found previously.

Let’s put everything together

How about calculating the velocity and position all together in the same while-loop?

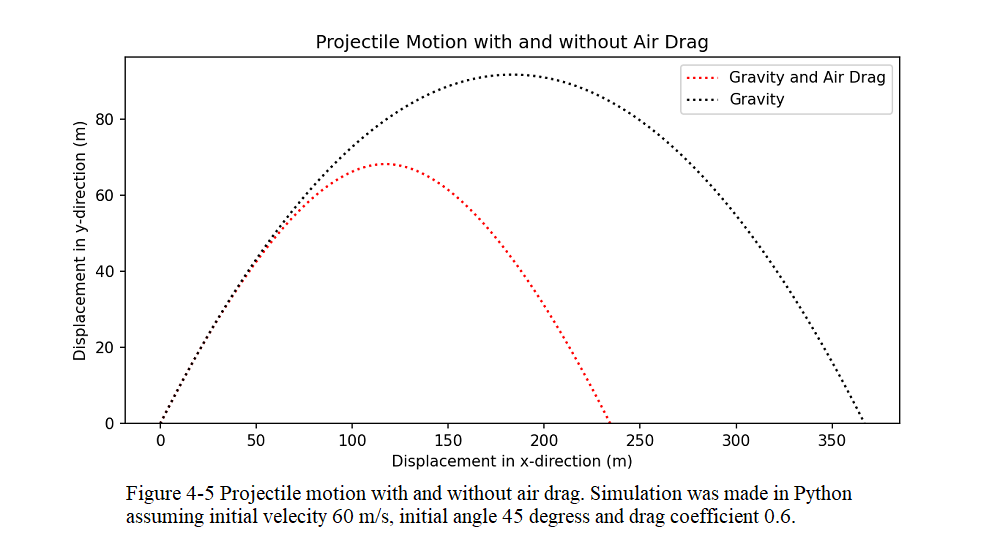
Also, let’s stop the while-loop after the projectile drops back to the ground again. One simple way to detect this is to check whether the value of y position falls below zero. So, we keep running the while-loop while \(y \geq 0\). In Fig. 4-5 show the projectile motion with and without air drag.

In deriving Eqn.4-6, we neglected the air resistance as a result it will give us a range much longer than we could have been expected considering the effect of air. Figure 4-13, for example, shows two paths for a fly ball that leaves the bat at an angle of 60° with the horizontal and an initial speed of 44.7 m/s. Path I (the baseball player’s fly ball) is a calculated path that approximates normal conditions of play, in air. Path II (the physics professor’s fly ball) is the path the ball would follow in a vacuum.

\(Table~ 4-1~ Two~ Fly~ Balls^a\)

	Path-I (Gravity & Air Drag)	Path-II (Gravity)
Range	234.69 m	366.97 m
Maximum height	68.24 m	91.74 m
Time of flight	7.11 s	8.64 s

Solved Problems:Motion in Two and Three Dimensions

1. [3] A positron undergoes a displacement \(\Delta \vec r= 2.0\hat i-3.0\hat j+6.0\hat k\), ending with the position vector \(\vec r = 3.0\hat j-4.0\hat k\), in meters. What was the positron’s initial position vector?

Given positron displacement of positron \[\Delta \vec r= 2.0\hat i-3.0\hat j+6.0\hat k\] and the final position of the positron \[\vec r_2 = 3.0\hat j-4.0\hat k\]

The initial position vector of positron can be found as follows:

\[\Delta\vec r = \vec r_2 - \vec r_1\] or

\[\vec r_1 = \vec r_2-\Delta\vec r=(3.0\hat j-4.0\hat k)-(2.0\hat i-3.0\hat j+6.0\hat k)=-2.0\hat i+6.0\hat j-10.0\hat k\space (Answer)\]

2. [11] The position \(\vec r\) of a particle moving in an xy plane is given by \(\vec r = (2.00t^3-5.00t)\hat i + (6.00-7.00t^4)\hat j\), with \(\vec r\) in meters and t in seconds. In unit-vector notation, calculate (a) \(\vec r\), (b) \(\vec v\), and (c) \(\vec a\) for t = 2.00 s. (d) What is the angle between the positive direction of the x axis and a line tangent to the particle’s path at t = 2.00 s?

1. Given \[\vec r = (2.00t^3-5.00t)\hat i + (6.00-7.00t^4)\hat j\] \[\vec r(t=2~s) = \left[(2.00)(2~s)^3-(5.00)(2~s)\right]\hat i + \left[(6.00)-(7.00)(2~s)^4)\right]\hat j\] \[=(6.0~m)\hat i-(106~m)\hat j\space (Answer)\]

2. \[\vec v=\frac{d\vec r}{dt}=(6.00t^2-5.00)\hat i + (-28.00t^3)\vec j\] \[\vec v(t=2~s)=\left[(6.00)(2~s)^2-5.00\right ]\hat i + \left[(-28.00)(2~s)^3)\right]\vec j=19\hat i-224\hat j~(Answer)\]

3. \[\vec a=\frac{d\vec v}{dt}=(12.00t)\hat i+(-84.00t^2)\hat j\] \[\vec a(t=2~s)=(12.00)(2~s)\hat i+(-84.00)(2~s)^2)\hat j=(24.00\hat i-336\hat j\space (Answer)\]

4. \[\theta = \tan^{-1}\left(\frac{-224}{19}\right)=-85.15^\circ~(Answer)\]

3. [13] A particle moves so that its position (in meters) as a function of time (in seconds) is \(\vec r=\hat i+4t^2\hat j+t\hat k\). Write expressions for (a) its velocity and (b) its acceleration as functions of time.

1. \[\vec v = \frac{d\vec r}{dt}=(8~m/s)t\hat j+(1~m/s)\hat k\]
2. \[\vec a = \frac{d\vec v}{dt}=(8~m/s^2)\hat j\]

4. [23] A projectile is fired horizontally from a gun that is 45.0 m above flat ground, emerging from the gun with a speed of 250 m/s. (a) How long does the projectile remain in the air? (b) At what horizontal distance from the firing point does it strike the ground? (c) What is the magnitude of the vertical component of its velocity as it strikes the ground?

1. Using Eq. 4-2, \[y-y_0=(v_0\sin\theta_0)t-\frac{1}{2}gt^2\] Since the projectile was fired horizontally, \(\theta_0=0\) \[0-y_0=(v_0\sin0^\circ)t-\frac{1}{2}gt^2\] \[t=\sqrt\frac{2y_0}{g}=\sqrt\frac{2(45~m)}{9.8~m/s^2}=3.03~s.\space (Answer)\]

2. Using Eq. 4-1, \[x-x_0=(v_0\cos\theta_0)t=(250~m/s)(cos0^\circ)(3.03~s)\approx758~m.\space(Answer)\]

3. Using Eq. 4-3, \[v_y=(v_0\sin\theta_0)-gt=(250~m/s)(\sin0^\circ)-(9.8~m/s^2)(3.03~s)=-29.69~m/s\] \[|v_y|=|-29.69~m/s|=29.69~m/s~(Answer)\]

5. [27] A certain airplane has a speed of 290.0 km/h and is diving at an angle of \(\theta = 30.0^\circ\) below the horizontal when the pilot releases a radar decoy (Fig. 4-6). The horizontal distance between the release point and the point where the decoy strikes the ground is d = 700 m. (a) How long is the decoy in the air? (b) How high was the release point?

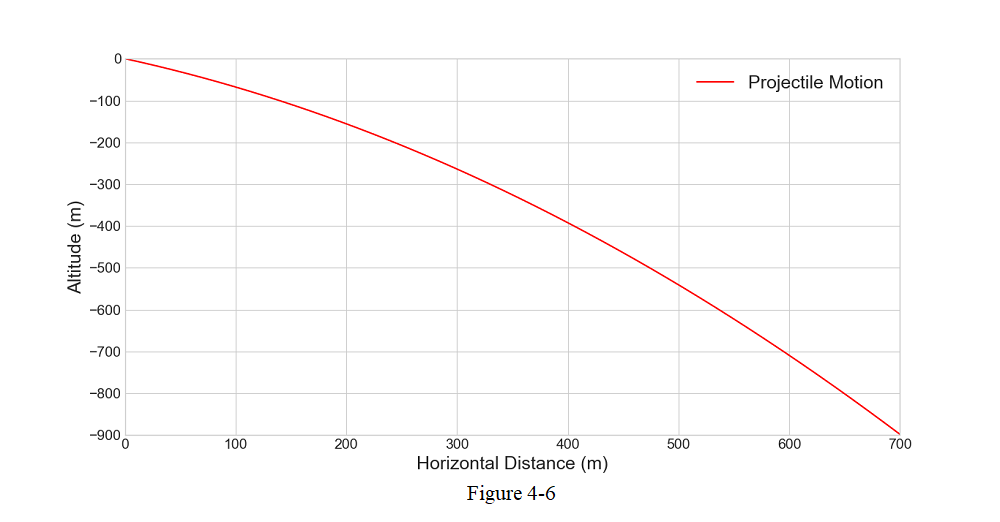
1. Time decoy was in the air: \[x-x_0=(v_0\cos\theta_0)t\] \[700~m=\left(\frac{290\times10^3~m/s}{3600}\right)(\cos30^\circ)t\] \[t=\frac{(700~m)(3600)}{(290\times 10^3~m/s)cos30^\circ}=10.03~s\space(Answer)\]

2. Height of decoy release point: \[y-y_0=(v_0\sin\theta_0)t-\frac{1}{2}gt^2\] \[y-0=-\left(\frac{290\times 10^3~m/s}{3600}\right)(\sin30^\circ)(10.03~s)-\frac{1}{2}(9.8~m/s^2)(10.03~s)^2\] \[y=-893~m\space(Answer)\]

6. [57] A carnival merry-go-round rotates about a vertical axis at a constant rate. A man standing on the edge has a constant speed of 3.66 m/s and a centripetal acceleration \(\vec a\) of magnitude 1.83 m/\(s^2\). Position vector \(\vec r\) locates him relative to the rotation axis. (a) What is the magnitude of \(\vec r\)? What is the direction of \(\vec r\) when \(\vec a\) is directed (b) due east and (c) due south?

1. \(r=\frac{v^2}{a}=\frac{(3.66~m/s)^2}{1.83~m/s^2}=7.32~m~(Answer)\)
2. West
3. North

7. [59] A woman rides a carnival Ferris wheel at radius 15 m, completing five turns about its horizontal axis every minute.What are (a) the period of the motion, the (b) magnitude and (c) direction of her centripetal acceleration at the highest point, and the (d) magnitude and (e) direction of her centripetal acceleration at the lowest point?

1. \(T=\frac{60~s}{5}=12~s\)
2. \(v=\frac{2\pi r}{T}=\frac{2\pi r(15~m)}{12~s}=7.85~m/s\)

\(a=\frac{v^2}{r}=\frac{(7.85~m/s)^2}{15~m}=4.11~m/s^2\)

3. downward

4. \(4.11~m/s^2\)

5. upward

8. [61] When a large star becomes a supernova, its core may be compressed so tightly that it becomes a neutron star, with a radius of about 20 km (about the size of the San Francisco area). If a neutron star rotates once every second, (a) what is the speed of a particle on the star’s equator and (b) what is the magnitude of the particle’s centripetal acceleration? (c) If the neutron star rotates faster, do the answers to (a) and (b) increase, decrease, or remain the same?

1. \(v=\frac{2\pi r}{T}=\frac{2\pi(20\times10^3~m)}{1~s}=1.26\times10^5~m/s\)

2. \(a = \frac{v^2}{r}=\frac{(1.26\times 10^5~m/s)^2}{20\times 10^3~m}=7.9\times10^5~m/s^2\)

3. increase

Problems:Motion in Two and Three Dimensions

Section 4-1 Position and Displacement

1. [1] The position vector for an electron is \(\vec r = (5.0 m)\hat i-(3.0 m)\hat j+(2.0 m)\hat k\). (a) Find the magnitude of \(\vec r\). (b) Sketch the vector on a right-handed coordinate system.

2. [2] A watermelon seed has the following coordinates: x = -5.0 m, y = 8.0 m, and z = 0 m. Find its position vector (a) in unit-vector notation and as (b) a magnitude and (c) an angle relative to the positive direction of the x axis. (d) Sketch the vector on a right-handed coordinate system. If the seed is moved to the xyz coordinates (3.00 m, 0 m, 0m),what is its displacement (e) in unit-vector notation and as (f) a magnitude and (g) an angle relative to the positive x direction?

Section 4-2 Average Velocity and Instantaneous Velocity

3. [5] A train at a constant 60.0 km/h moves east for 40.0 min, then in a direction \(50.0^\circ\) east of due north for 20.0 min, and then west for 50.0 min. What are the (a) magnitude and (b) angle of its average velocity during this trip?

4. [6] An electron’s position is given by \(\vec r = 3.00t\hat i-4.00t^2\hat j+2.00\hat k\), with t in seconds and in meters. (a) In unit-vector notation, what is the electron’s velocity \(\vec v(t)\)? At t 2.00 s, what is \(\vec v\) (b) in unitvector notation and as (c) a magnitude and (d) an angle relative to the positive direction of the x axis?

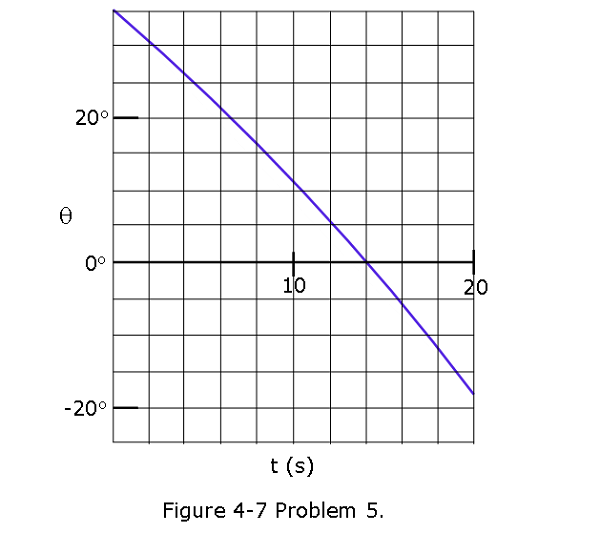
5. [10] The position vector \(\vec r = 5.00t\hat i+(et + ft^2)\hat j\) locates a particle as a function of time t. Vector \(\vec r\) is in meters, t is in seconds, and factors e and f are constants. Figure 4-7 gives the angle \(\theta\) of the particle’s direction of travel as a function of t (\(\theta\) is measured from the positive x direction).What are (a) e and (b) f, including units?

Section 4-3 Average Acceleration and Instantaneous Acceleration

6. [14] A proton initially has \(\vec v = 4.0\hat i-2.0\hat j+3.0\hat k\) and then 4.0 s later has \(\vec v = -2.0\hat i-2.0\hat j+5.0\hat k\) (in meters per second). For that 4.0 s, what are (a) the proton’s average acceleration \(\vec a_{avg}\) in unit vector notation, (b) the magnitude of \(\vec a_{avg}\), and (c) the angle between \(\vec a_{avg}\) and the positive direction of the x axis?

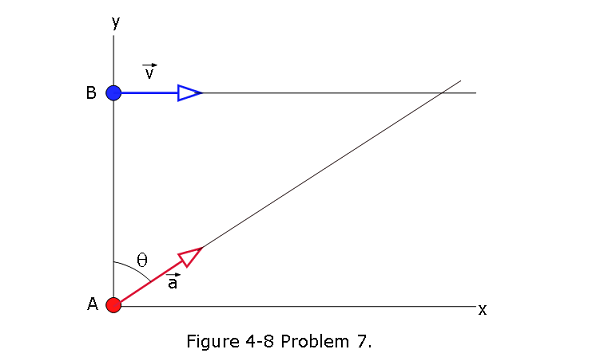
7. [20] In Fig. 4-8, particle A moves along the line y = 30 m with a constant velocity \(\vec v\) of magnitude 3.0 m/s and parallel to the x axis. At the instant particle A passes the y axis, particle B leaves the origin with a zero initial speed and a constant acceleration \(\vec a\) of magnitude \(0.40 m/s^2\). What angle \(\theta\) between \(\vec a\) and the positive direction of the y axis would result in a collision?

Section 4-4 Projectile Motion

8. [21] A dart is thrown horizontally with an initial speed of 10 m/s toward point P, the bull’s-eye on a dart board. It hits at point Q on the rim, vertically below P, 0.19 s later. (a)What is the distance PQ? (b) How far away from the dart board is the dart released?

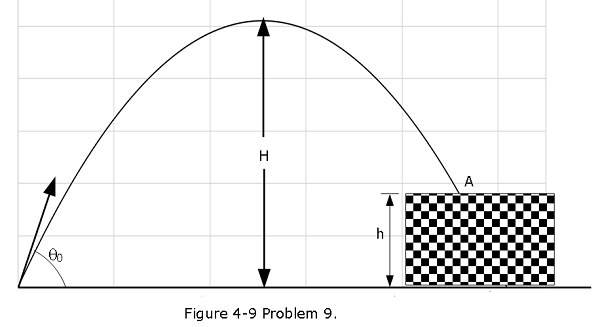
9. [28] In Fig. 4-9, a stone is projected at a cliff of height h with an initial speed of 42.0 m/s directed at angle \(\theta_0 = 60.0^\circ\) above the horizontal. The stone strikes at A, 5.50 s after launching. Find (a) the height h of the cliff, (b) the speed of the stone just before impact at A, and (c) the maximum height H reached above the ground.

10. [33] A plane, diving with constant speed at an angle of \(53.0^\circ\) with the vertical, releases a projectile at an altitude of 730 m. The projectile hits the ground 5.00 s after release. (a) What is the speed of the plane? (b) How far does the projectile travel horizontally during its flight? What are the (c) horizontal and (d) vertical components of its velocity just before striking the ground?

11. [42] In 1939 or 1940, Emanuel Zacchini took his humancannonball act to an extreme: After being shot from a cannon, he soared over three Ferris wheels and into a net (Fig. 4-10). Assume that he is launched with a speed of 26.5 m/s and at an angle of \(53.0^\circ\). (a) Treating him as a particle, calculate his clearance over the first wheel. (b) If he reached maximum height over the middle wheel, by how much did he clear it? (c) How far from the cannon should the net’s center have been positioned (neglect air drag)?

Section 4-5 Uniform Circular Motion

12. [58] A rotating fan completes 1200 revolutions every minute. Consider the tip of a blade, at a radius of 0.15 m. (a) Through what distance does the tip move in one revolution? What are (b) the tip’s speed and (c) the magnitude of its acceleration? (d) What is the period of the motion?

13. [60] A centripetal-acceleration addict rides in uniform circular motion with radius r = 3.00 m. At one instant his acceleration is \(\vec a = (6.00 m/s^2)\hat i + (-4.00 m/s^2)\hat j.\) At that instant, what are the values of (a) \(\vec v.\vec a\) and \(\vec r \times \vec a.\)

14. [62] What is the magnitude of the acceleration of a sprinter running at 10 m/s when rounding a turn of radius 25 m?

Section 4-6 Relative Motion in One Dimension